
分数の計算ときくと、
苦手に感じてしまう
小中学生の皆さんも
いるのではないでしょうか。
分数の計算、中でも
“通分”は
小学校5年生で勉強する
算数の単元。
教科書でも
取り上げられているように
日常の場面
●1本のテープを等分する
●正方形のブロック(レゴ)を帯状につなげて説明
●ブロックのポッチを活かして説明
●アナログ時計と時計の針を使って解説
などに変えて
勉強することが
“わかる”ようになる
一番の近道です。
ただ、
どんな方法を使うと
わかりやすいかは、
生徒さん一人一人
ちがうのです。
そこでこちらの記事では、
する方法を解説します。
苦手な人でも
すんなり理解できるよう、
スモールステップでの説明を
心掛けました。
自分のペースで勉強したい
小中学生の皆さんや
丁寧な説明が欲しい
保護者様向けに
基本から説明しています。
記事を書いたのは、

●小中学生対象完全個別指導塾の校長(経営者兼専任講師)
●開校5年半で、新潟県内トップ私立高校合格者を輩出。
●年評定平均:中学時代3点台→高校進学後4.9、4.8、4.4の塾生を輩出。
●サポートした不登校の卒塾生、大学へ進学(卒業)。
●オリジナル直筆記事が、グーグル3ワード検索で1位(2024.4.1現在)
●当ブログ、にほんブログ村カテゴリー「中学受験(個人塾)」
で、2020年6月から36ヶ月以上ランキング1位。
2020年3月開設15ヵ月目で月間4万PV超。
●元公立高校教員
●現役カウンセラー
こと“のびのび”。


目次【タップでジャンプ】
分数の計算|分子が1のとき

まずは、
分数の上の数字
分子が両方“1”
のときです。
分数の計算|分子が1の足し算(加法)
簡単な例題をつかって、
わかりやすく解説します。
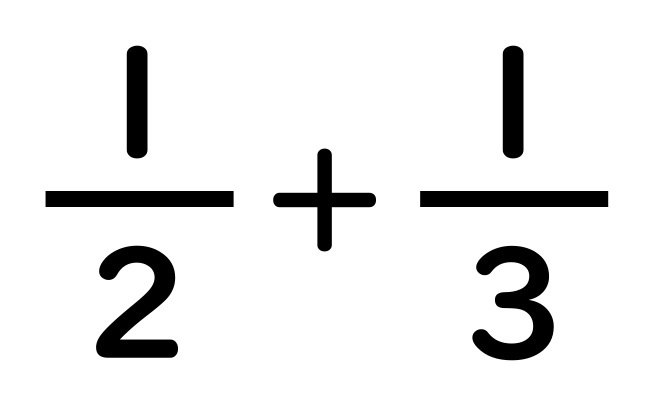
イメージしやすくするために、
それぞれの分数を
2種類のピザ=円を
使ってあらわしてみました。


円の色味は、
サラミ系のピザと
照り焼き系のピザ。
この2枚のピザを使って
分数の計算“通分”を説明
していきます。
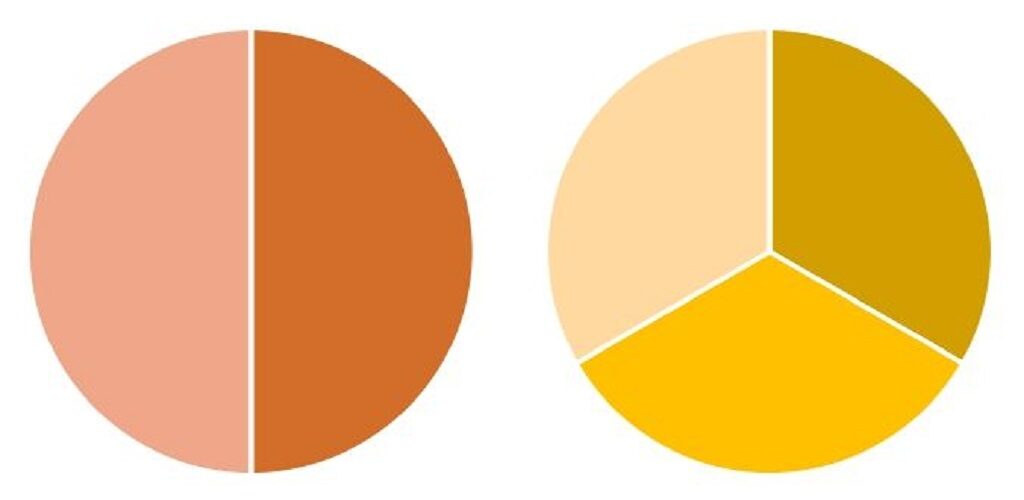
まず、
それぞれのピザを、
それぞれの分母
“2”と“3”で
切り分けます。
お友達に
おすそわけする分は、
冷蔵庫に入れました。
ですので、
例題の分だけ残りました。

このままでは、
形が違うので
足したあとの
量はわかりません。
そこでまず、
同じ形に切りなおします。
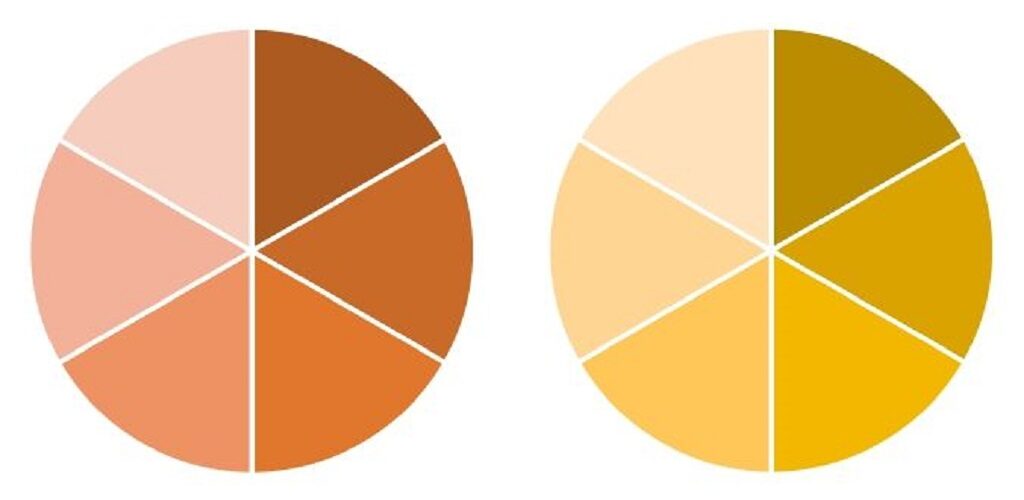
両方とも同じ大きさに分けるには、
分母どうしをかけた数
2×3=6
6等分に切りなおします。
冷蔵庫に入れた分を
とりのぞくと、
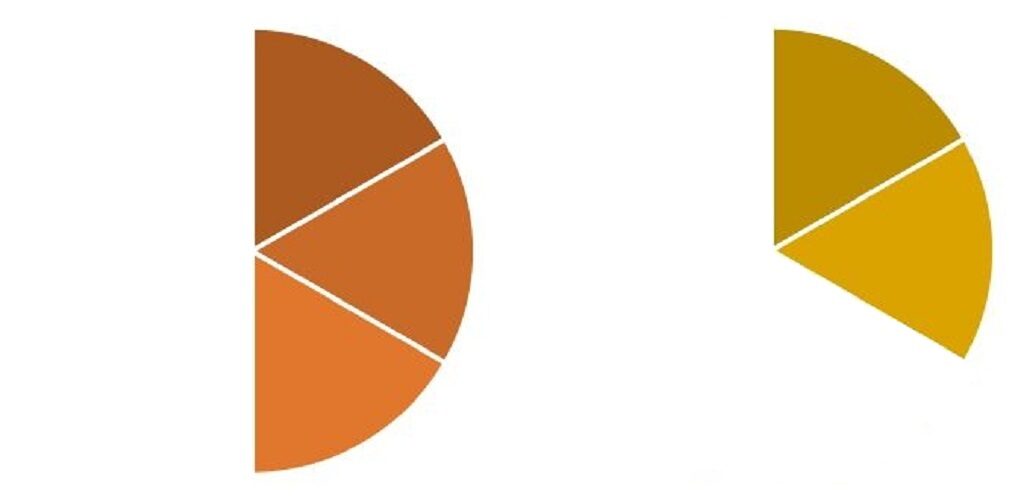

上と下を見くらべてみてください。
3/6(6分の3)は、1/2(2分の1)、
2/6(6分の2)は、1/3(3分の1)、
それぞれ同じ大きさである
ことがわかると思います。
こうすれば、
1切れサイズはすべて同じ大きさに
なりますので、
足した後の量もわかります。
右のピザを
180度(半円分)回転させて、
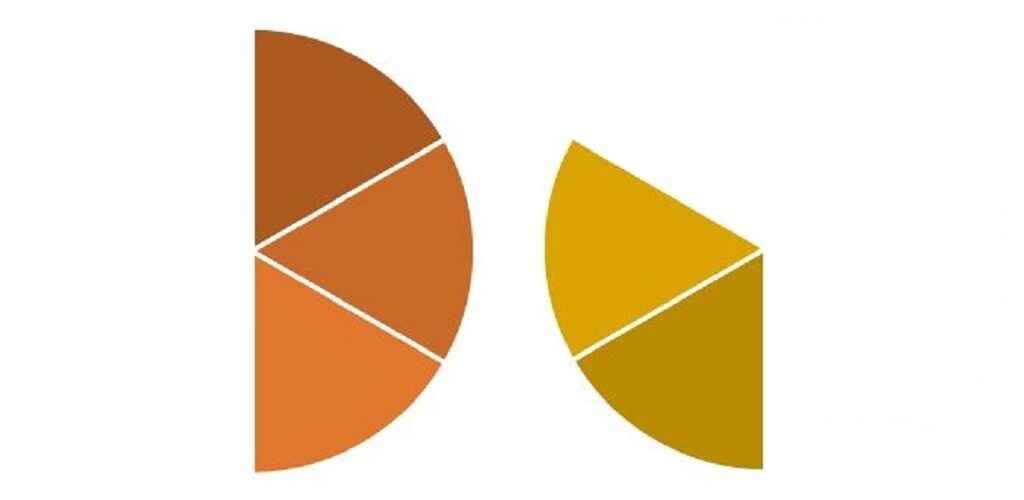
くっつけると、
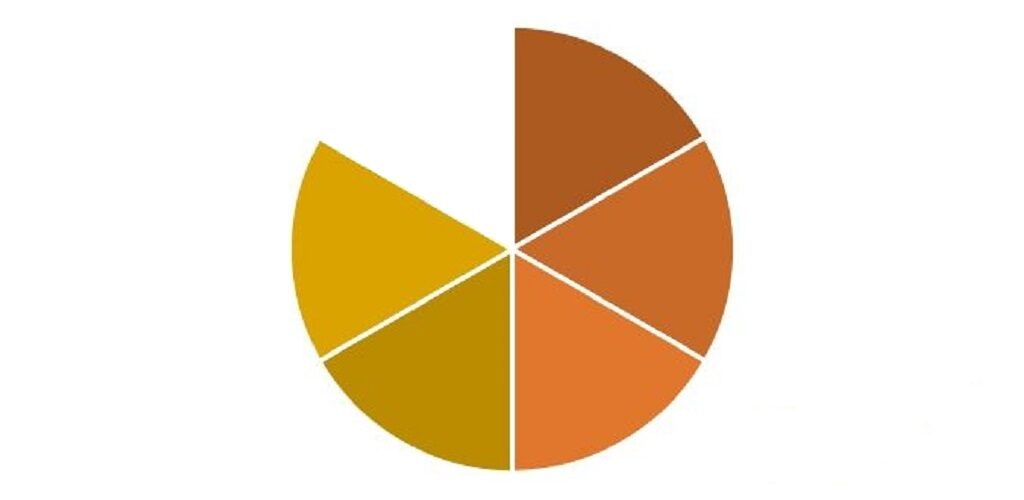
5切れになりました。
1枚のピザ=円
(1=6/6、6分の6)
のうち5切れですので、
答えは5/6(6分の5)。
これを計算の式に
書きなおすと、
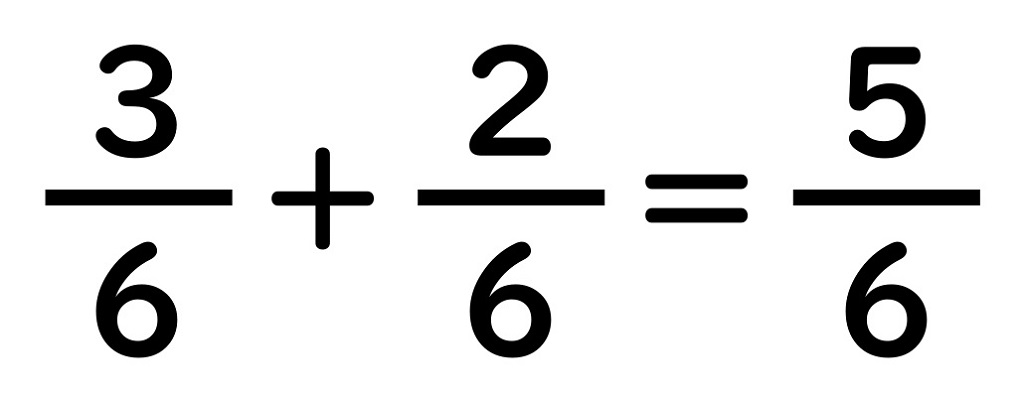
となります。
分数の計算|分子が1のひき算(減法の練習問題)
では分子が1のときの
引き算は
どうなるでしょうか。
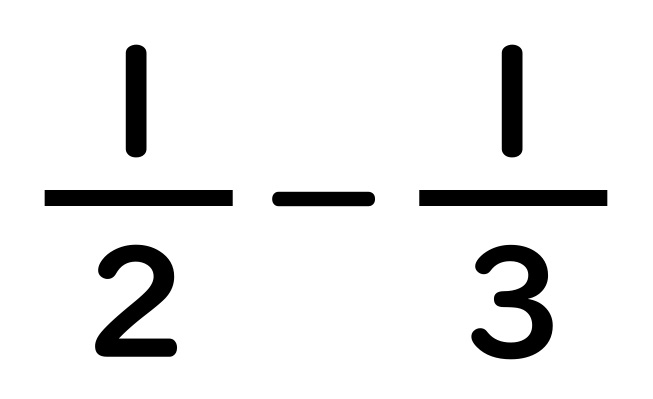
足し算の例題の
記号を変えただけ
です。
たした時と同じように、
6つに切りなおして
計算してみてください。

なっていると思います。
本文とは関係ありません。
分数の計算|分子が1でないとき

つぎに、
分子が1でないとき
を見ていきましょう。
分数の計算|分子が1でない足し算(加法)
今回も
例題で見ていきます。
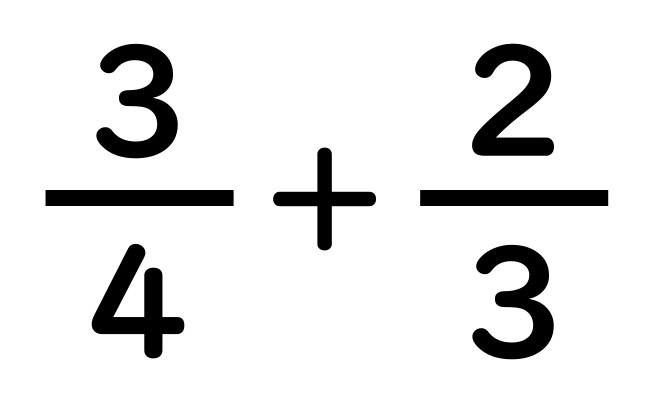
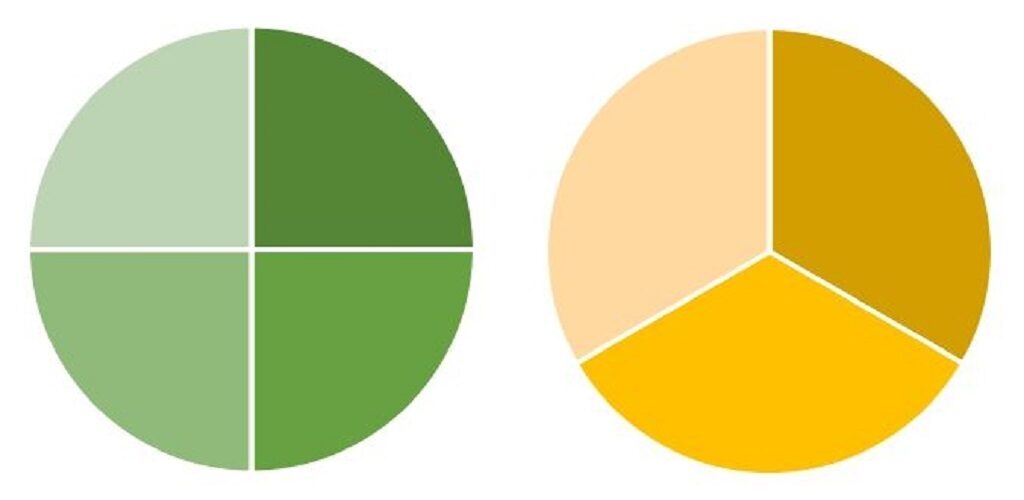
プレゼントの分は、
冷蔵庫にいれましたので、
例題の分だけ残りました。
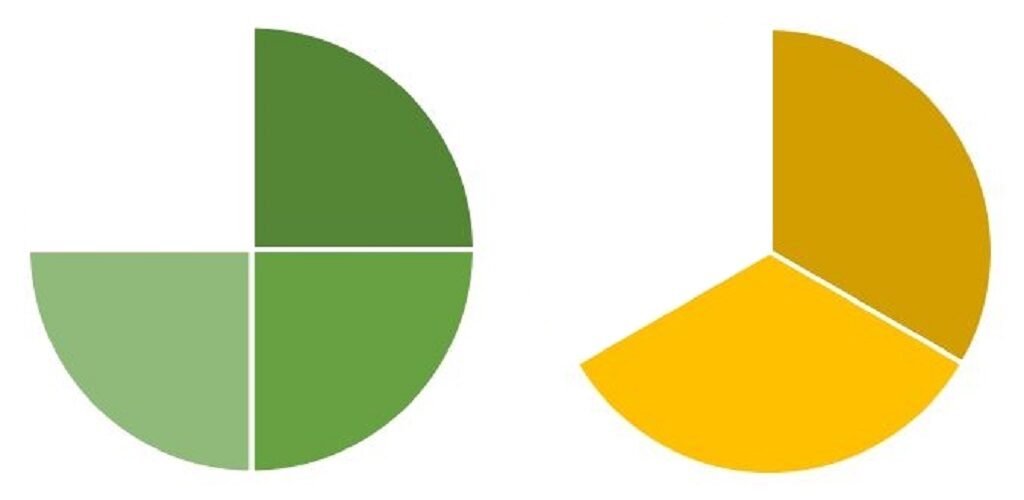
一切れの大きさが
違いますので、
このままでは
計算できません。
なので、
同じ形に切りなおし
ます。
両方とも同じ
1切れサイズにするには、
分母どうしをかけた数
4×3=12
12等分に切りなおします。
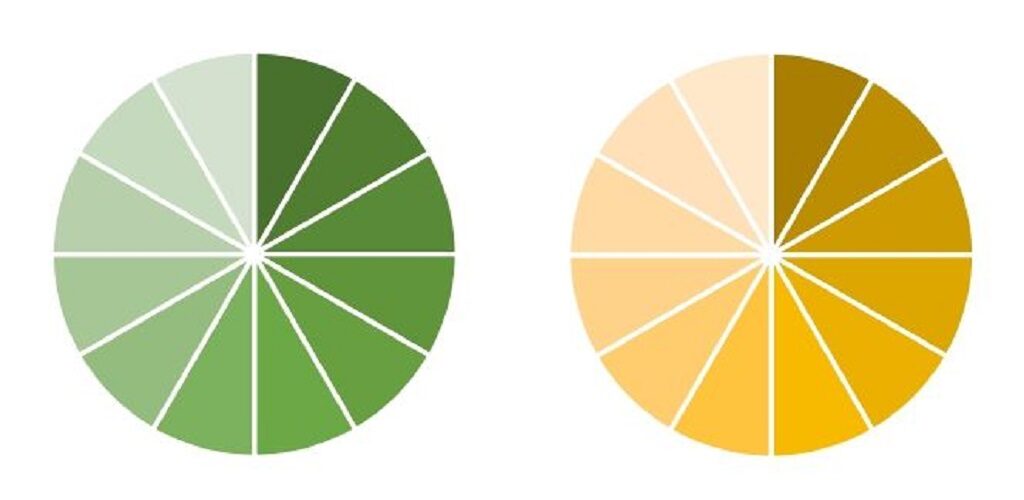

小さすぎじゃない?

何切れも食べてください~
さっきと同じ分だけ、
冷蔵庫にしまうと、
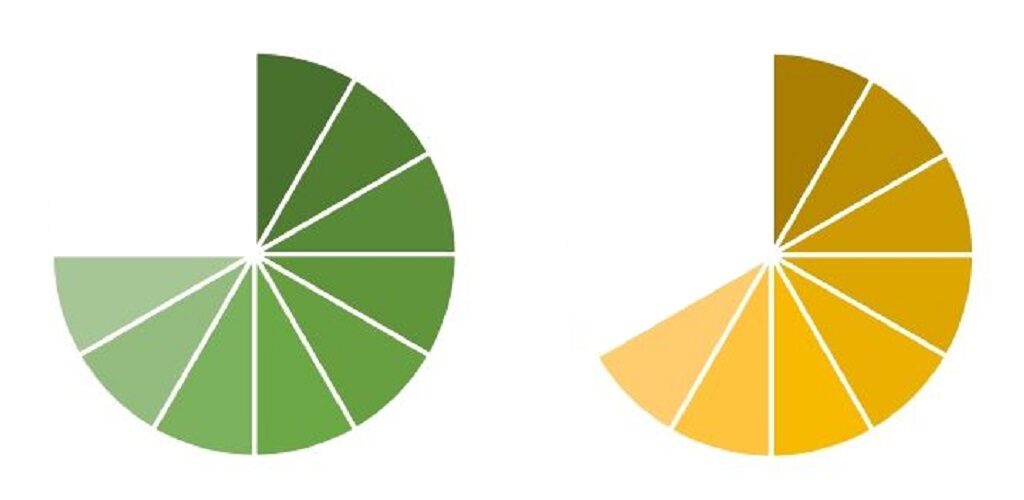

上と下を見くらべてみてください。
9/12(12分の9)は、3/4(4分の3)、
8/12(12分の8)は、2/3(3分の2)、
それぞれ同じ大きさ
だとわかると思います。
これで、2つのピザとも
1切れの大きさは
みんな同じになりました
ので、計算できます。

数えると17切れ。
ですので、
答えは17/12(12分の17)。
これを計算の式に
書きなおすと、
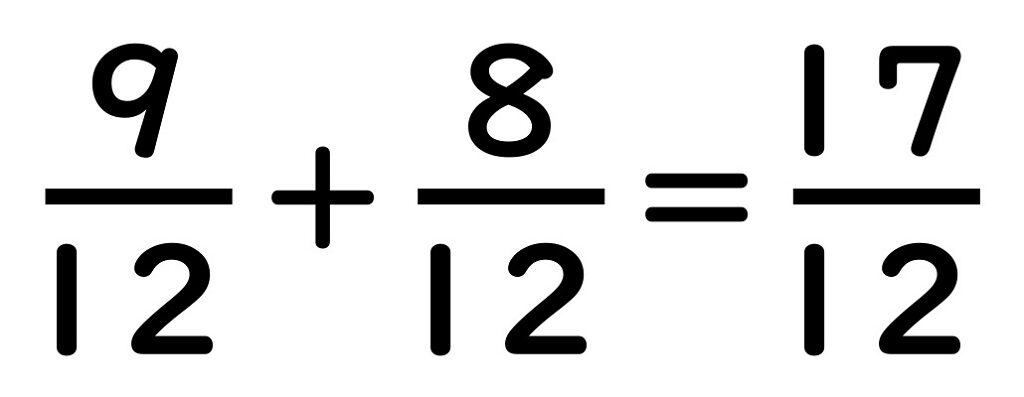
となります。
分子が分母より大きい
数になりました。
これを
“仮分数(かぶんすう)”
といいます。
分母より分子が小さい分数は
“真分数(しんぶんすう)”
といいます。
整数と真分数が
くっついている分数を
“帯分数(たいぶんすう)”
といいます。
答えが
仮分数になったときは、
帯分数に
なおしてみましょう。
右のピザを、
時計と反対回りに
90度(直角分)回転
させて、
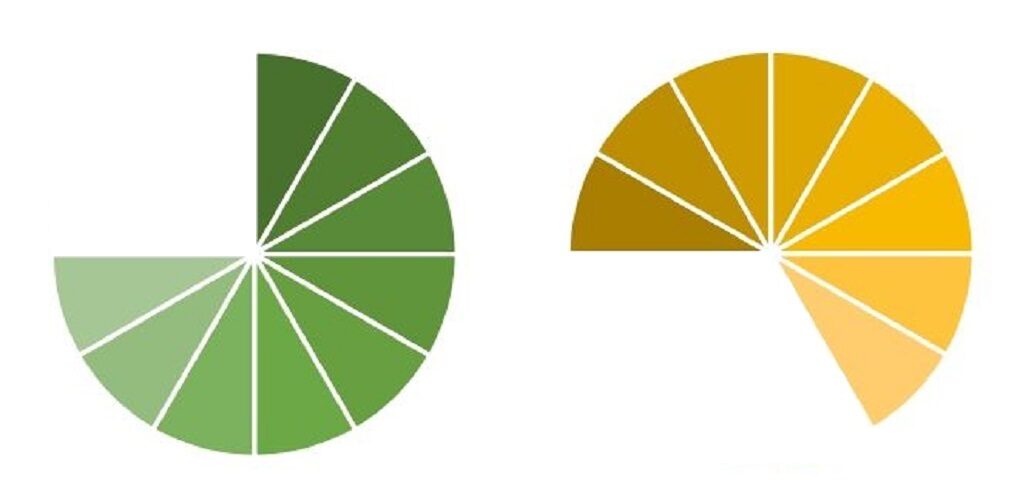
左のピザに
右のピザを
3切れくっつけ
ます。すると…
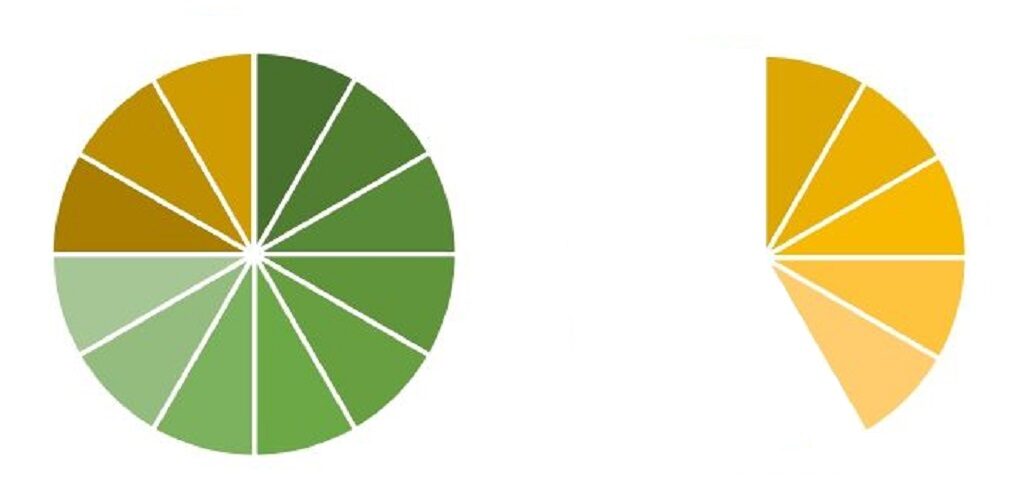
1枚のピザと5切れ
になりました。
これを式であらわすと、
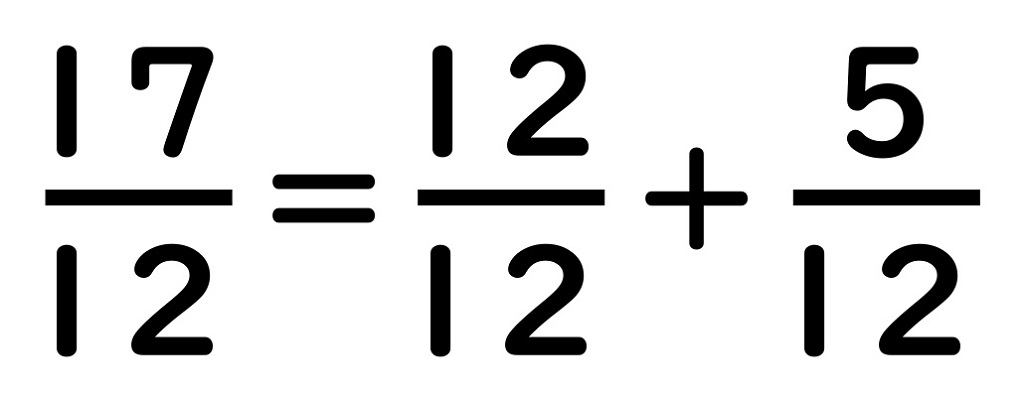
となります。
12個に分けたものを
12個集めれば、
もとの1枚に
なりますので、
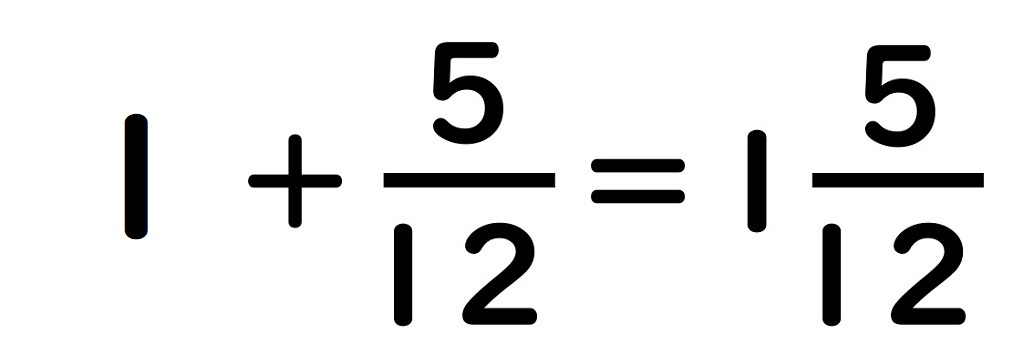
このように仮分数を
帯分数であらわすことも
できるのです。
分数の計算|分子が1でないひき算(減法の練習問題)
では、引き算は
どうなるでしょうか。
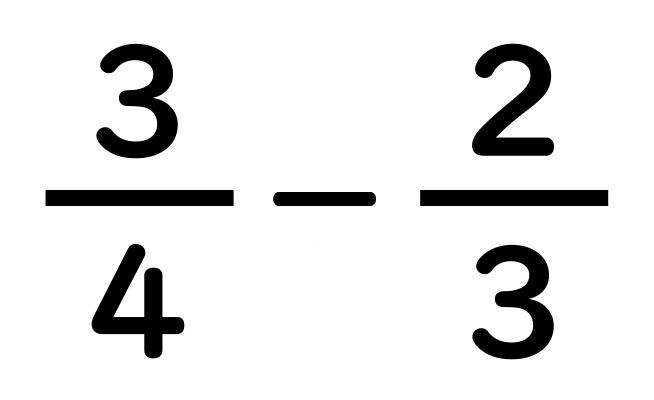
これも計算の
記号を変えただけです。
たした時と同じように
切りなおして
計算してみてください。

できるようになっている
と思います!
分数の計算 まとめ

こちらの記事では、
する方法を解説してきました。
今回は、円(ピザ)を使って
分母の違う分数の計算
“通分”を説明しましたが、
これ以外にも日常の場面
●正方形のブロック(レゴ)を帯状につなげて説明
●ブロックのポッチを活かして説明
●アナログ時計と時計の針を使って解説
など、別の具体例を使った方が

と感じる生徒さんも
いると思います。
どんな方法を使うと
わかりやすいかは、
生徒さん自身が
やってみないとわからないもの。
イメージしやすい、
アウトプットしやすい、
自分がやりやすい方法で
練習すれば、
苦手を克服しやすくなります。
ぜひ色々試して工夫して、
苦手克服に
つなげていただければ
と思います。

幸いです。
最後までお読みいただき
ありがとうございました。
分数の通分が苦手な人向け計算テクニックは、下記の記事をご参照ください。
教室の取り組みは、下記の記事をご参照ください。















