
中学の数学では、図形の学習で立体の表面積や体積を勉強しますが、新潟市の個別指導塾スクールNOBINOBIの塾生さんの中にも、苦手に感じる生徒さんが多い単元です。
そこでこちらの記事では、図形の学習に苦手意識をもつ生徒さん向けに、円錐の表面積の出し方“3つの方法”を
●円錐の側面積を楽に計算する方法
●円錐の表面積を一発で計算する公式

●開校5年半で、新潟県内トップ私立高校合格者を輩出。
●年評定平均:中学時代3.7→高校進学後4.9、4.8の塾生を輩出。
●サポートした不登校の卒塾生、大学へ進学。
●当ブログ、にほんブログ村カテゴリー「中学受験(個人塾)」
で、2020年6月から14ヶ月連続ランキング1位。
2020年3月開設15ヵ月目で月間4万PV超達成。
●元公立高校教員
●現役カウンセラー
こと“のびのび”が自作のイラストと図で、わかりやすく丁寧に解説。
忘れにくい方法、一発で計算する公式もご紹介していきますので、
自分にあった方法で、円錐の表面積の問題を楽々クリアしてもらいたい!
と考えています。
目次【タップでジャンプ】
円錐(えんすい、直円錐)とは?

円錐(えんすい)とは、平面上の円の円周上の各点と、その平面上にない一点とを結んでできる立体。
中が空っぽの円錐は側面と底面の2つのパーツでできています。
中学の数学で勉強する円錐は、底面の円の中心と頂点とを結ぶ線が、底面に垂直な直円錐(ちょくえんすい)です。垂直にならない円錐は、斜円錐(しゃえんすい)といいます。
直円錐は、アイスのコーン(cone)、工事現場などに置かれるカラーコーンの台座をとった部分、鉛筆の先、大工道具のキリ、建物の屋根などをイメージしてもらえればわかりやすいかと思います。
ここでは、直円錐を円錐と呼んで解説していきます。
まずイメージしてもらいやすくするために、中身が空っぽの円錐の見取り図と展開図、パーツの名前と記号をご紹介します。
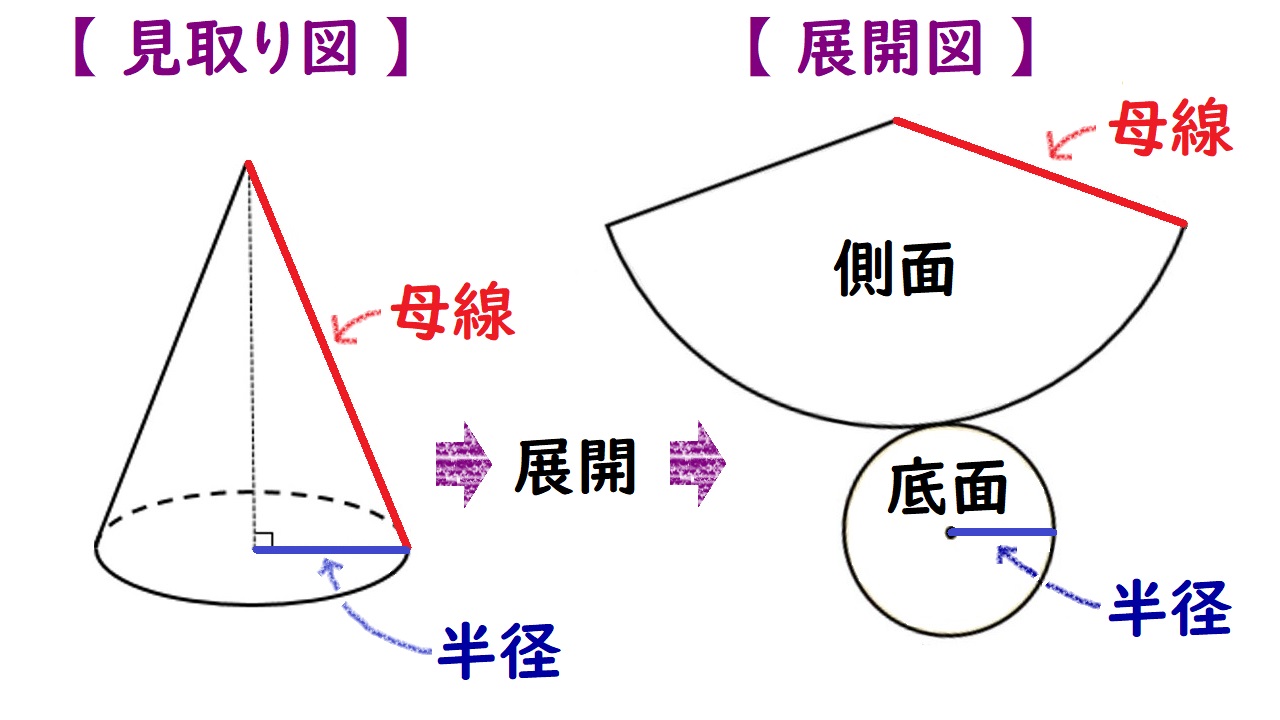
ちなみに、
側面の面積は側面積
底面の面積は底面積
といいます。
円錐の表面積の出し方、基本の計算方法

円錐の表面積は“側面積+底面積”で求めることができます。
紙でできた円錐の側面を切って広げると、円の一部である“扇形”になります。
こちらの記事で、紙で自作した円錐と展開写真を確認できます。
扇形の中心角がわかると、円に対して側面の扇形がどれくらいの割合(比率)になるか、がわかります。
ですから、まず、扇形の中心角を求めると良いのです。
それでは、例題を使って順番に見ていきましょう。
例題)次の円錐の表面積を求めましょう。
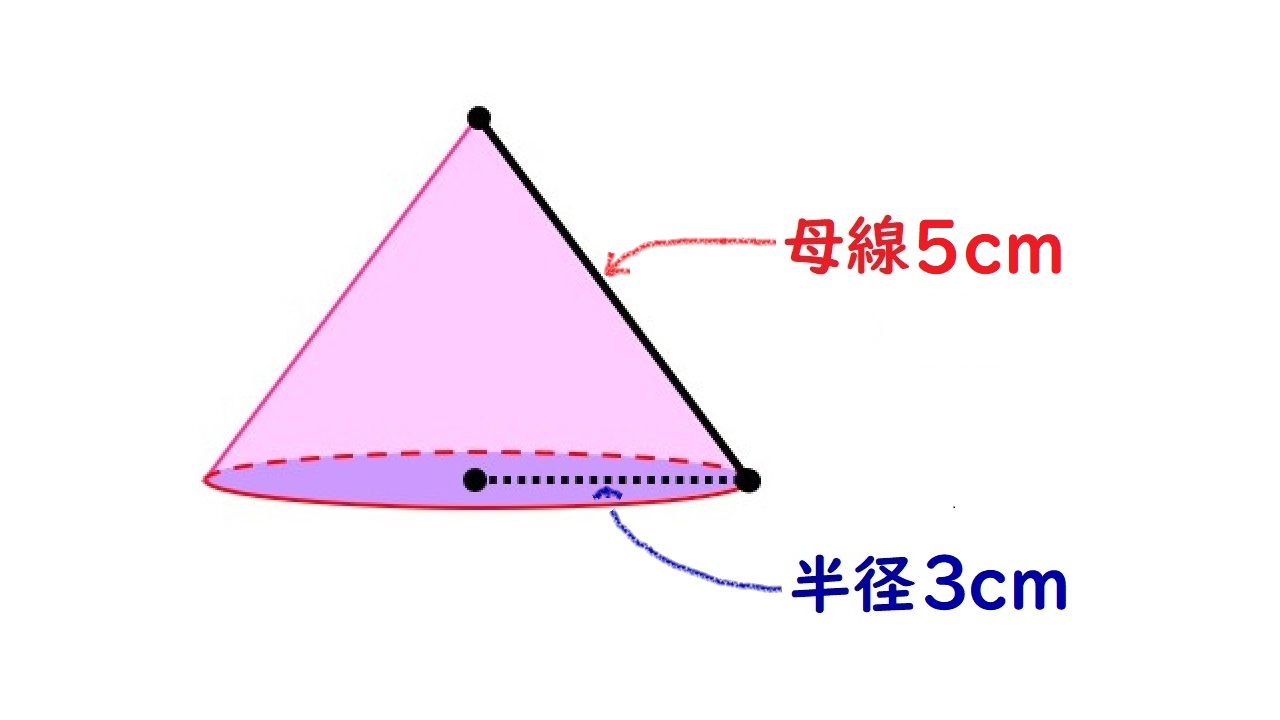
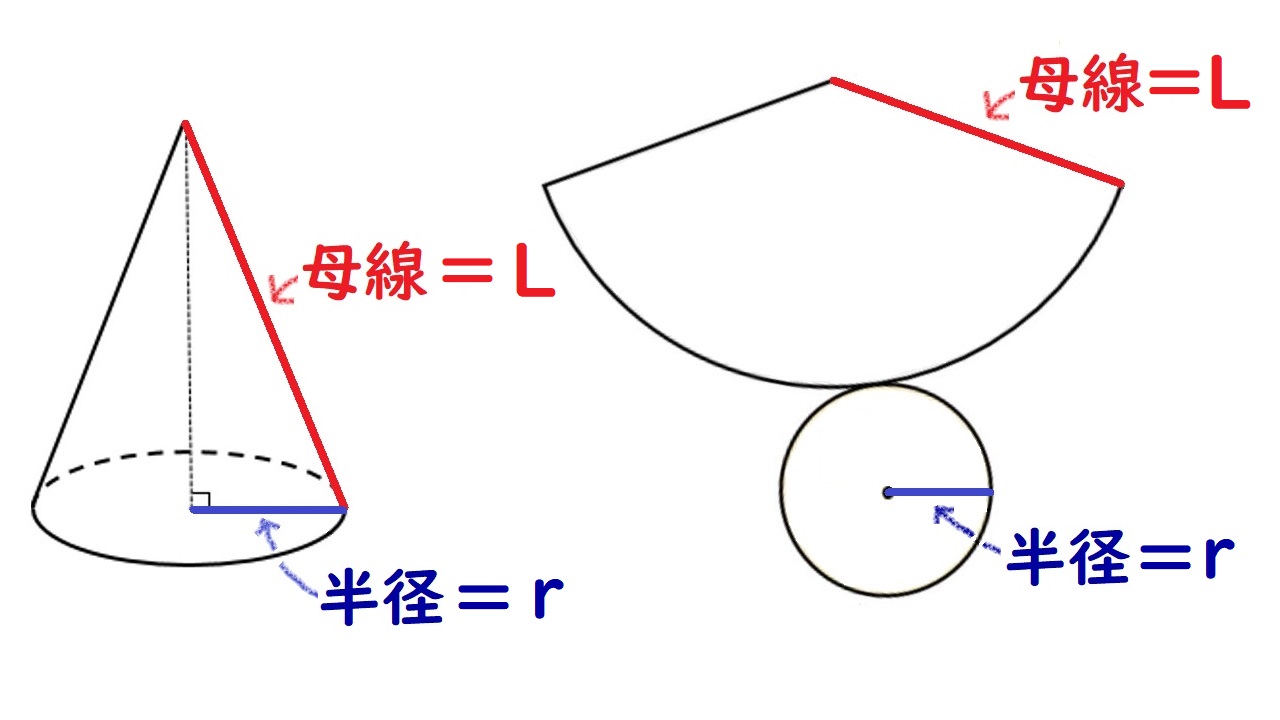
この円錐を母線と底面の縁にそって切りひらく(展開する)と、
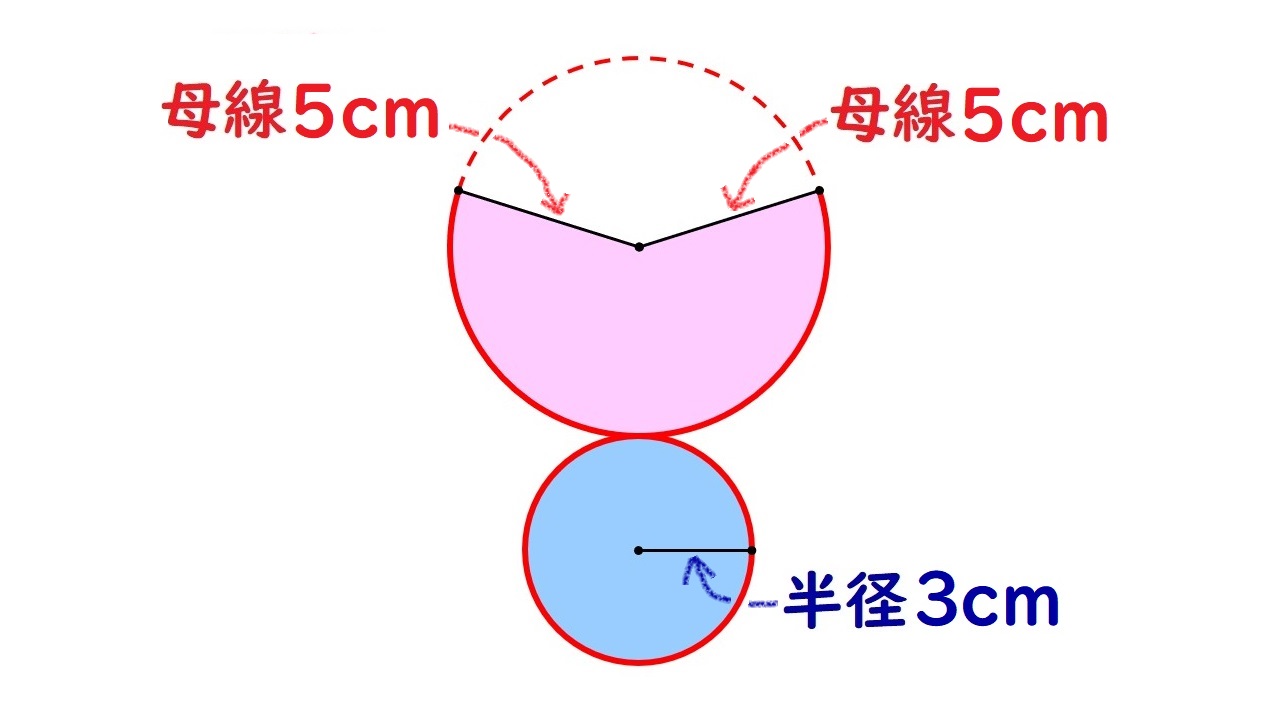
こんな形になります。
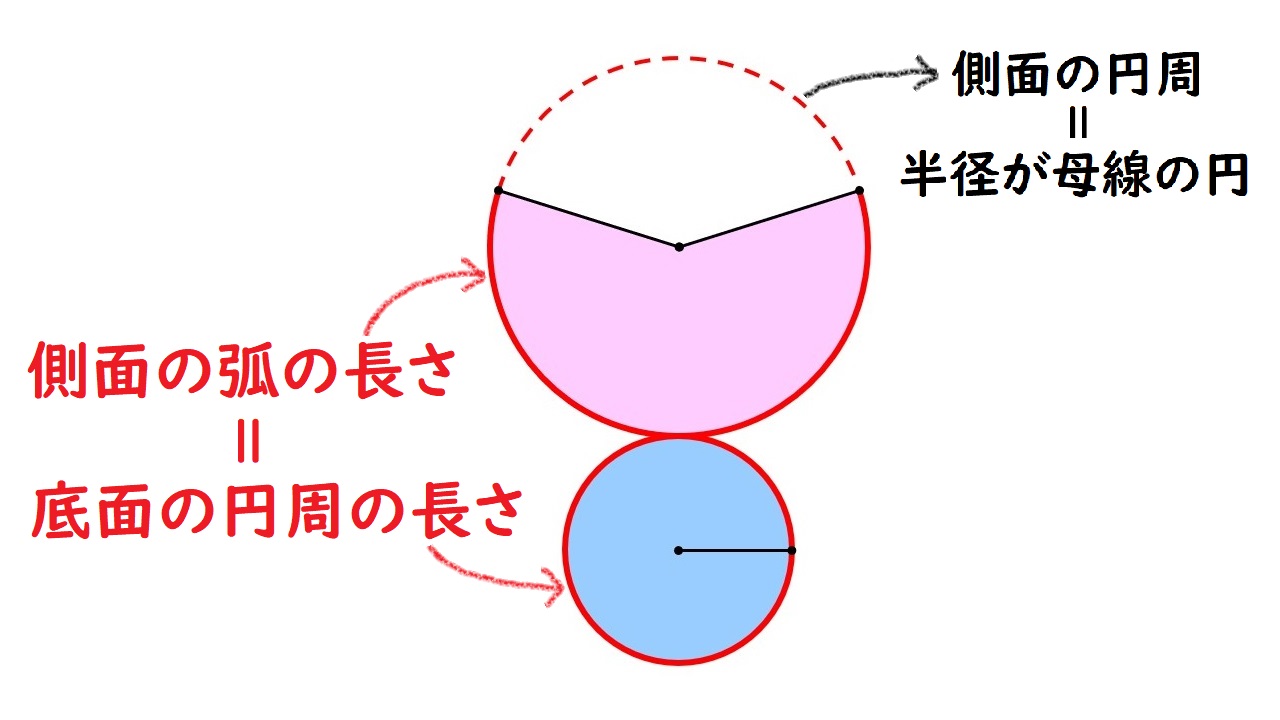
扇形の弧の長さと底面の円周の長さ(赤い線の部分)は、ぴったり同じ長さになります。
円の円周の長さは、
直径×円周率 = 半径(r)の2倍×円周率(π)= 2πr
ですので、この円錐の底面の円周の長さは
3×2×π=6×π
6π㎝となります。
側面の扇形を円にした(図のように赤い点線でつなげた)ときの円周の長さに対して、側面の赤い実線の弧の長さがどのくらいの割合になるかわかれば、円の角度360°に対する扇形の中心の角度“中心角”の割合がわかり、中心角の大きさを求めることができるのです。
“側面の母線を半径とする円”に対して、側面の扇形の弧の長さ、中心角、面積は、ぜんぶ同じ割合。

となるのです。
この円錐の底面の円周の長さは6π㎝でしたので、
側面の扇形の弧の長さも、同じ長さの6π㎝。
“側面の円”は母線が半径になりますので、5㎝。
“側面の円”=“側面の母線を半径とする円”の円周の長さは、
5×2×π=10π
10π㎝になります。
扇形の弧の長さは、円周10π㎝のうちの6π㎝ですので、
割合は6/10(十分の六)、約分すると3/5(五分の三)になります。
先ほどの式のように、割合はぜんぶ同じですので、
中心角は360°の3/5、216°となります。
扇形の面積“側面積”も同様に、円の面積の3/5になります。
円の面積の出し方は
半径×半径×円周率=半径(r)×半径(r)×円周率(π)=πr²
π×5×5=25π㎝²
25π㎝²の3/5が扇形の側面積の広さですので、
25π×3/5=15π㎝²
これに底面積の広さを合わせれば、円錐全体の表面積になるのです。
底面積は、
π×3×3=9π㎝²
この2つの面積を合計
15π㎝²+9π㎝²=24π㎝²
この円錐の表面積は、24π㎝² と計算できました。
円錐の側面積だけを、もっと簡単に計算する方法

これまで見てきた通り、側面の弧の長さと底面の円周の長さは等しくなりますから、

となります。

そこで両辺の2とπを消して、


さらに、両辺を“側面の母線”で÷と、

となります。
扇形の側面積は、
円周率(π)×母線²×中心角/360
で出せました。
先ほどの式で、
中心角/360=底面の半径/母線
となることが解りましたので、
扇形の側面積=円周率(π)×母線²× 中心角/360
の式の“中心角/360”を“底面の半径/母線”と入れかえてみます。
円周率(π)×母線²× 底面の半径/母線
円周率(π)×母線×母線× 底面の半径/母線
“×母線”で“÷母線”が打ち消せますので、
円周率(π)×母線×底面の半径
が残ります。
結果、
となるのです。
例題の円錐の側面積をこの公式で計算すると、
π×5×3=15π
15π㎝²
あっという間に円錐の側面積が出せました!
これに底面積をプラスすれば、円錐全体の表面積も簡単に出せるのです。
円錐全体の表面積を、もっともっと簡単に計算する公式

先ほどの
円錐の側面積の簡単な出し方を使って、円錐の表面積の出し方の公式を導き出す
こともできます。
円錐の側面積に円錐の底面積をあわせれば、円錐の表面積ですので、
円錐の側面積+円錐の底面積
円周率(π)×母線×底面の半径 + 円周率(π)×底面の半径²
円周率(π)×母線×底面の半径 + 円周率(π)×底面の半径×底面の半径
となるはずです。
“円周率”と“底面の半径”は、ともに側面と底面の両方にかけられていますので“単元:文字と式”で勉強したように()を使ってまとめることができます。

記号でおきかえると、
となります。
例題の円錐の表面積なら、
π×3×(5+3)
=π×3×8=24π
24π㎝²
側面の母線と底面の半径がわかる円錐の表面積なら、

まとめ

こちらの記事では、円錐の表面積の出し方“3つの方法”を、
●円錐の側面積を楽に計算する方法
●円錐の表面積を一発で計算する公式
の順で解説してきました。
個人的に一番わかりやすく忘れにくいと思うのは、
なのですが、生徒さんの理解の仕方は人それぞれ。
自分にあった方法で、円錐の表面積の問題を楽々クリアしてもらいたい!と考えています。
おまけクイズ
では、例題の円錐の高さは何㎝になるでしょうか?
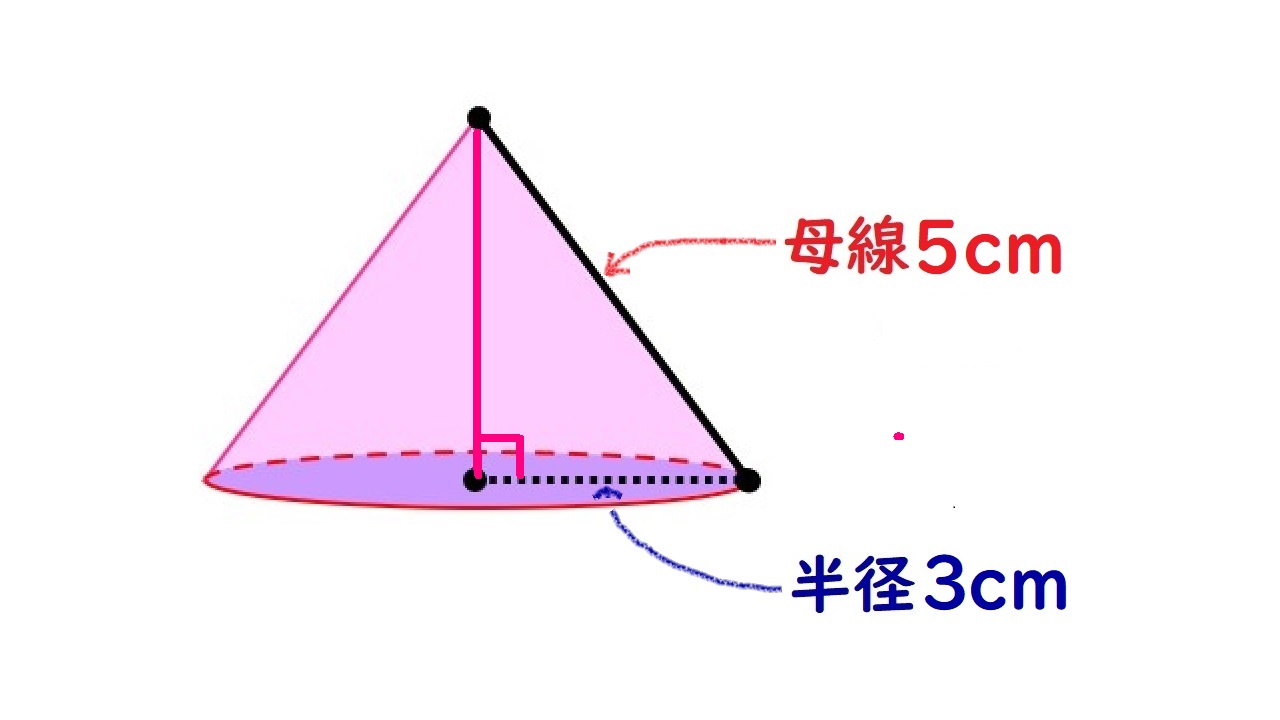
中学3年生の皆さんは学校の授業で学習すると思いますが、
中学1年生、中学2年生の皆さんも覚えておいて損はないと思います。
答えはこの記事の最後を確認してください。

最後までお読みいただきありがとうございました。
おまけクイズ解答

底辺:高さ:斜辺の比が、3:4:5の直角三角形もあるのです。














