
中学2年生の数学では、一次関数を勉強します。
これまで、新潟市の個別指導塾スクールNOBINOBIの塾生さん達から

という声を、何度も聞いてきました。
そこでこちらの記事では、一次関数の文章問題に苦手意識をもつ生徒さん向けに、
代表的な問題の解き方を

●開校5年半で、新潟県内トップ私立高校合格者を輩出。
●年評定平均:中学時代3.7→高校進学後4.9、4.8の塾生を輩出。
●サポートした不登校の卒塾生、大学へ進学。
●当ブログ、にほんブログ村カテゴリー「中学受験(個人塾)」
で、2020年6月から17ヶ月連続ランキング1位。
2020年3月開設15ヵ月目で月間4万PV超達成。
●元公立高校教員
●現役カウンセラー
こと“のびのび”が、自作の図とグラフでわかりやすく丁寧に解説。
テストに良く出る問題の解き方もご紹介しますので、
ぜひ最後までお付き合いください。
目次のタイトルをタップすると、読みたい場所に移動できます。
目次【タップでジャンプ】
一次関数の文章問題の解き方|重要ポイント

はじめに、大切なポイントをまとめました。
一次関数、解き方のポイント
- 問題文から“ x ”と“ y ”になるものを見つける。
- xとyをつかって式をつくる。
- あとで y = ax + b の形に変えればいい。
- 途中でグラフが変わる場合は、変わるポイントで分けて考える。
- グラフは、1めもりの単位に注目。
の5つです。
再確認ポイント、4つ
- 一次関数の公式は、y = a x + b
- a = 傾き = 変化の割合 = 定数 = 比例定数 = xの変化量分のyの変化量
- b = 切片 = 定数 = xがゼロの時のyの値 = y軸とグラフの交点
- a も b も、それぞれ 変わらない数 = 定数
一次関数の文章問題でいちばん大切なのは、解き方ポイント1の
“ x “と“ y “になるものを見つけだすこと。
問題文の中に
「 x と y の関係を表す式を求めなさい 」
「 yをxの式で表しなさい 」
と出てくる文章題は、一次関数の問題、と言うこともできます。
※二次関数の問題もあります。
一次関数、テストによく出る出題パターンと解き方

よく出る出題パターンと、それぞれの解き方は、
- 問題文にx と y がでてくるパターン
【解き方】
そのまま素直に公式にあてはめる。 - 時間で値が変わるパターン
【解き方】
時間をx、時間によって変化する値(長さ距離、量、面積など)をyとする。 - 問題に「〇〇は(が)□□の一次関数」とでてくるパターン
【解き方】
○○を y 、□□を x とする。
の3つ。
他に良く出るだけでなく、間違いやすい「動点の問題」も解説します。
一次関数3つの出題パターン、それぞれの解き方を解説

よく出る出題パターンの解き方、それぞれ見ていきます。
1.問題にx と y がでてくるパターン

【 解き方のポイント 】
そのまま素直に公式にあてはめる。
家から80㎞はなれた親戚のおじさんの家まで、原付バイクで遊びにいくことにした。全ての道のりを平均時速25㎞で走行。家を出発してからx時間後の、おじさんの家までの残りの道のりをy㎞とする。
x と y の関係を式に表しなさい。
解き方
家を出発してからx時間後の、おじさんの家までの残りの道のりをy㎞とします。
全体の道のりから、x 時間で進んだ道のり(距離)を引けば残りの道のり y がわかるから、
y= 80 - 25 x
あとで y = ax + b の形に変えればいいので、
y=-25x + 80
となります。

変域を問われたら?
x 、y の変域を問われることもあります。
変域は、x 、y の最少と最多がわかればOK。
x は時間でしたので、
最短時間は、出発地点の“ 0 ”、
最長時間は、80㎞走り切るのにかかった時間。
時間 = 距離 ÷ 速さ
最長時間 = 80 ÷ 25
最長時間 = 3.2(= 3+1/5時間 = 3時間12分)
なので、x の変域は、
0 ≦ x ≦ 3.2(3+1/5)、0時間以上3時間12分以下となります。
yは距離でしたので、変域は、
先ほど求めた x の変域の最少「0」と最大「4」を
それぞれ一次関数の式に代入すれば求められます。
y=-25 × 0 + 80
y= 0 + 80
y= 80(㎞)
y=-25 × 3.2 + 80
y= 80 + 80
y= 0(㎞)
なので、y の変域は
0 ≦ y ≦ 80 、0㎞以上80㎞以下となります。
2.時間で値が変わるパターン

【 解き方のポイント 】
時間を x 、時間によって変化する値(長さ距離、量、面積など)を y とする。
水が60L入った水槽を掃除したいので、一旦全てぬくことにした。なくなるまで一定の割合で水をぬいていく。水をぬき始めてから8分後の水の量は、50Lのめもりのところだった。
yを x の式で表しなさい。
解き方
もともとあった水の量60Lからぬいた分の水を引けば残りの水量がわかるはずです。
解き方ポイントのとおり、
時間を x
時間によって変わる値 = 残りの水量 = y
とすると、式は
y= 60 - a x
時間あたり(この場合は1分)でぬける水の量は、一定(定数=a)です。
これ(a)がわかれば
yを x の式で表す = 一次関数の式をつくる
ことができます。
問題文にでてくる「8分後に残り50L」、
これを先ほどつくった式に代入すると…
50 = 60 - 8 a
計算すると
8a = 60 - 50
8a = 10
8a/8 = 10/8
a = 5/4
定数 a がわかったので、yを x の式で表すと、
y= 60 - 5/4 x
y=-5/4 x + 60
となります。
ちなみに x の変域は
0 ≦ x ≦ 48、0分以上48分以下、
y の変域は
0 ≦ y ≦ 60 、0L以上60L以下
となります。
3.問題に「〇〇は(が)□□の一次関数」とでてくるパターン

【 解き方のポイント 】
○○を y 、□□を x とする。
友だちを呼んで、ホットケーキをつくってみんなで食べたい!ホットケーキにつけるハチミツとホイップクリームも用意してセットにしたい!と親に相談したら、
3人分のセットを用意するには、1,300円
5人分のセットを用意するには、2,500円
の費用がかかる、と言われました。
ホットケーキ・セットにかかる費用は、食べる人数の一次関数です。
友だち6人と自分をあわせた7人分のホットケーキ・セットを用意するのにかかる費用を求めなさい。
解き方
解き方ポイントのとおり、
ホットケーキ・セットにかかる費用は、食べる人数の一次関数だから、
ホットケーキ・セットにかかる費用 = 〇〇 = y
食べる人数 = □□ = x
わかっていること全部つかって式をつくると、
1300=3a+b
2500=5a+b
の2つの式ができます。
連立方程式の加減法を使って、b を消せば a が求められるのです。
2500 =5a+b
1300 =3a+b
1200 =2a
1200/2 = 2a/2
a = 600
わかった a をどちらかの式に代入すれば、b がわかります。
1300 = 600×3 + b
1300 = 1800 + b
b = -500
一次関数は
y = 600 x - 500
となります。
7人分を求めるので、xに7を代入すれば費用を求めることができます。
4.動点の問題 解き方
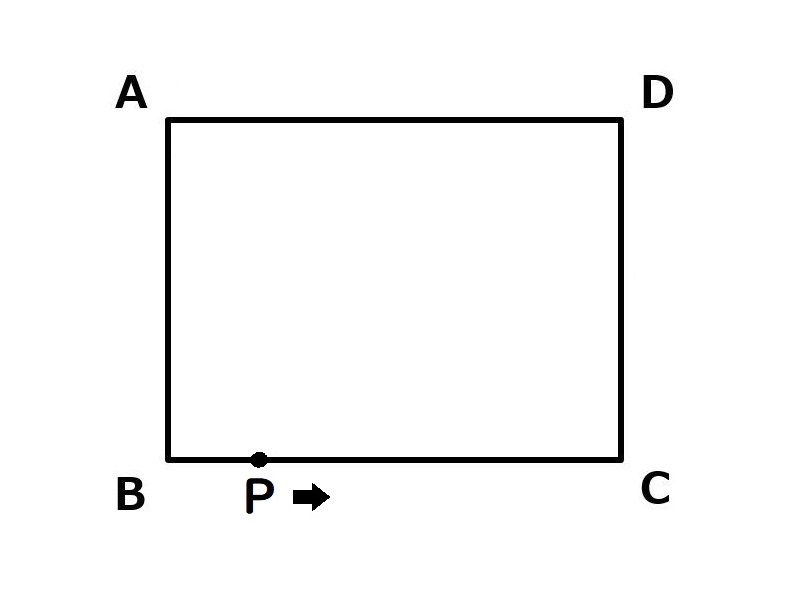
良く出されて間違いやすい「動点の問題」も解説します。
タテの長さが3cm、横の長さが4cmの長方形ABCDの周上を、点Pは毎秒1cmの速さで、AからB、Cを通ってDまで移動します。
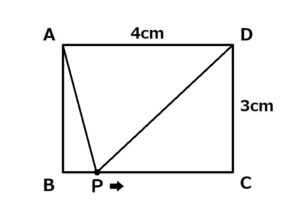
PがAを出発してからx秒後の△APDの面積をy cm²とするとき、yはxの変化にともなってどう変化するのか説明しなさい。
解き方
最初に説明した解き方ポイント4「途中でグラフが変わる場合は、変わるポイントで分けて」考えると…
- Pの場所で三角形の高さが変わる。底辺はどんなときも変わらない。
高さの変化がわかれば、面積が計算できる。 - Pの位置によって、3つのパターンに分けて考える。
- 三角形の“底辺”と“パターンごとの高さ”をしっかり確認する。
例題では、x 秒後の△APDの面積を y cm²とする、となっています。
この場合、△APDの底辺ADは変わりません。
Pが動くことで、△APDの高さは変わっていく、
Pが動くことで、移動時間(と距離) x はのびていく
のです。
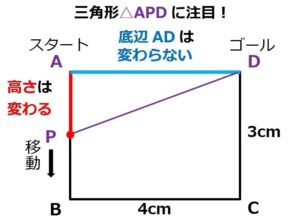
高さは、角をこえて次の辺に移動するたびに変わります。
なのでパターンは、点Pが辺AB、辺BC、辺CDにあるときの3つになります。
パターン1:点Pが、辺AB上にあるとき
点Pは1秒で1cm動きます。
なので点Pは、スタートからx秒後に、Aからx cmのところにあることになります。
△APDの高さはAPの距離。APの距離を x とすると、
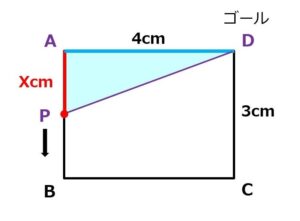
点Pが辺AB上にあるとき(0 ≦ x ≦3、xが0以上3以下)の△APDの面積は、
△APD = 底辺 × 高さAP × 1/2
= 4 × x × 1/2 = 2 x
y = 2 x
ここまでの△APDの面積yの変化をグラフにすると、
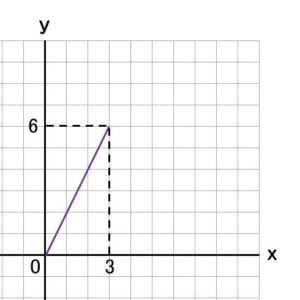
こうなります。
パターン2:点Pが辺BC上にあるとき
つぎに点Pは、Bを通過して、辺BC上を動きます。
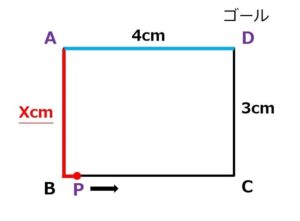
点Pが辺BC上にあるとき、△APDの高さは、点Pから底辺ADにおろした垂線。
Pからの垂線(赤い点線)と辺ADの交点をHとすると、PHが高さになります。
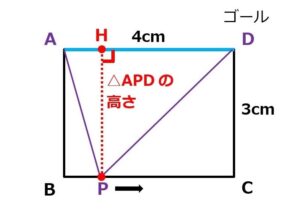
この高さは、B寄りでも…
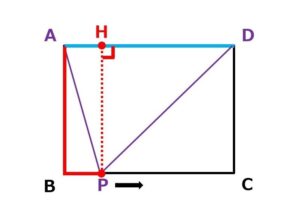
真ん中でも…
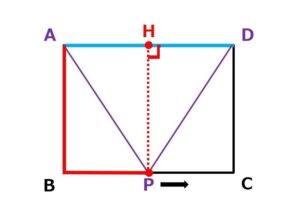
C寄りでも…
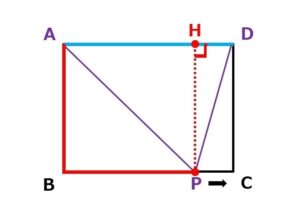
変わらないのです。
△APDの高さは、辺AB・辺DCと同じ長さですから、3cm。
そうすると、点Pが辺BC上にあるとき(3 ≦ x ≦ 7、xが3以上7以下)の△APD の面積は、
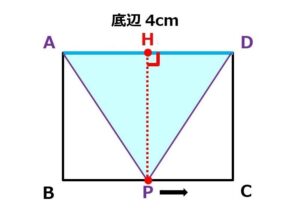
底辺AD × 高さPH × 1/2
= 4 × 3 × 1/2 = 6cm²
y = 6
点Pが辺BC上にあるとき、△APDは、Pがどこにあっても同じ面積
なのです。
スタート地点Aからここまでの、△APDの面積の変化をグラフにあらわすと、
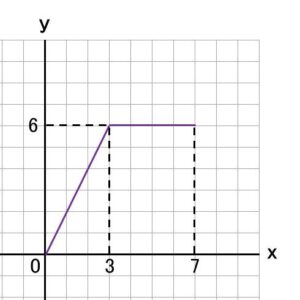
となります。
パターン3:点Pが辺CDにあるとき
最後に点Pは、Cを通過して、辺CD上を動きます。
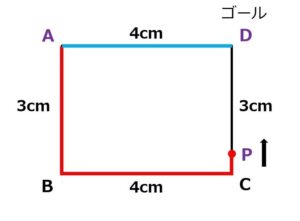
このパターンのときの△APDの高さはDPです。
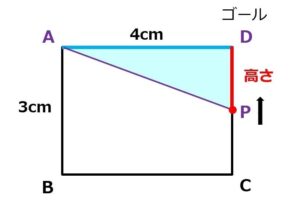
DPの距離がわかれば、△APDの面積がだせるはずです。
点Pが移動する距離は、辺AB、辺BC、辺CD。
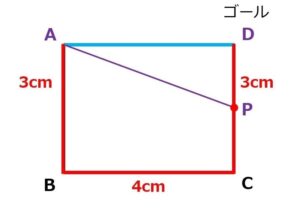
点Pの全ての移動距離は、3つの辺の長さの合計だから
3 + 4 + 3 = 10 cm
x秒後に点Pが動いた距離は、x cm。
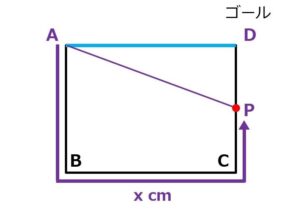
このときの△APDの高さDPは、
辺AB、辺BC、辺CDの合計から、点Pが動いた距離 x を引けば求められるはずです。
高さ = DPの長さ = 3つの辺の長さ - Pが動いた距離 なので、
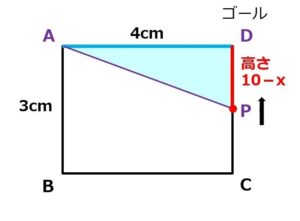
DP = 10 - x
そうすると、
点Pが辺AB上にあるとき(7 ≦ x ≦10、xが7以上10以下)の△APDの面積は、
底辺AD × 高さDP × 1/2
= 4 × ( 10 - x ) × 1/2
= 2 ( 10 - x )
y = 20 - 2x
スタートからゴールまでをグラフに表すと、
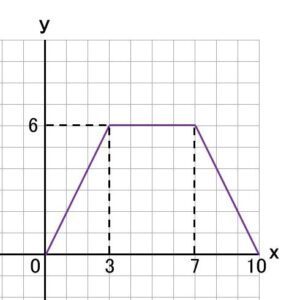
パターン : 1 2 3
3つのパターンごとに、△APDの面積 y と x を使って表せて、グラフが書ければ完璧です。
ちなみに x の変域は
0 ≦ x ≦ 10、0分以上10秒以下、
y の変域は
0 ≦ y ≦ 6 、0 m² 以上 6 m² 以下
となります。
まとめ

一次関数の文章問題の解き方のポイントは、
- 問題文から“x”と“y”になるものを見つける。
- xとyをつかって式をつくる。
- あとで y = ax + b の形に変えればいい。
- 途中でグラフが変わる場合は、変わるポイントで分けて考える。
- グラフは、1めもりの単位に注目。
の5つ。
一次関数の基本、再確認ポイントは、
- 一次関数の公式は、y = ax + b
- a = 傾き = 変化の割合 = 定数 = 比例定数 = xの変化量分のyの変化量
- b = 切片 = 定数 = xがゼロの時のyの値 = y軸とグラフの交点
- a も b も、それぞれ 変わらない数 = 定数
の4つ。
そして、いちばん大切なのは解き方ポイント1の“ x “と“ y “になるものを見つけだすことでした。
また、動点の文章問題の解き方ポイントは、
一次関数の解き方ポイント4「途中でグラフが変わる場合は、変わるポイントで分けて」考え、さらに、
- Pの場所で三角形の高さが変わる。底辺はどんなときも変わらない。
高さの変化がわかれば、面積が計算できる。 - Pの位置によって、3つのパターンに分けて考える。
- 三角形の“底辺”と“パターンごとの高さ”をしっかり確認する。
の3つのポイントに注目する、でした。

と言う塾生さんに


と気づいてくれます。
読解力が壊滅的に不足しているのでなければ、
こちらの記事で解説したポイントを意識して、
しっかり問題文を読むだけで
一次関数の文章問題の多くをスラスラ解けるようになるはず!
解ければ、高得点が期待できる文章問題。
まずは、こちらで取りあげた例題のような基本的な問題にチャレンジして
「できる感覚」をつかむことから始めてみてはいかがでしょうか。
読んでくださった中学生の皆さんの
得点力アップにつながることを心から願っています。














