
分母の違う分数を
たしたりひいたりするのに
使う“通分(つうぶん)”。
“分数の通分”は、
文部科学省の新学習指導要領で
小学校5年生で勉強
する算数の単元。
小学校、中学校、高校など
学生時代だけでなく
社会に出ても意外と使う
通分ですが、
新潟市のマンツーマン個別指導塾
スクールNOBINOBIに通う
小中学生の塾生さんの中にも

と感じる生徒さんがいます。

なってもらいたい!



記事の内容は
“バタフライ・フラクション”
=通称“ちょう分数(ちょうちょ分数)”
と呼ばれる通分方法を、ていねいに解説
記事を書いたのは、

●小中学生対象完全個別指導塾の校長(経営者兼専任講師)
●開校5年半で、新潟県内トップ私立高校合格者を輩出。
●年評定平均:中学時代3点台→高校進学後4.9、4.8、4.4の塾生を輩出。
●サポートした不登校の卒塾生、4年制大学卒業。
●オリジナル直筆記事が、グーグル2ワード検索で1位(2025.5.1現在)
●当ブログ、にほんブログ村カテゴリー「中学受験(個人塾)」
で、2020年6月から22ヶ月連続ランキング1位。
2020年3月開設15ヵ月目で月間4万PV超。
●元公立高校教員
●現役カウンセラー
こと“のびのび”。

わかりやすく解説します!
目次【タップでジャンプ】
分数の通分|誰でも使えるテクニック

こちらの記事でご紹介する
分数の通分に役立つテクニックは、
“バタフライ・フラクション”
日本語で
“ちょう分数(ちょうちょ分数)”
と呼ばれる通分の方法です。
学校授業のように
具体的な事例
(たとえば、2種類のピザをみんなで分ける)で
“わかる”ようになってもらってから、
計算方法に進む方が良いのです。
ですが、
具体例で理解がぼんやりしたまま
のお子さんがいても、
学校のカリキュラムは
どんどん進みます。
そんな理解しにくかった皆さんにも
イメージしやすく、
正しい答えを導いてくれるのが
この“バタフライ・フラクション”。
数学先進国インドの公教育でも
使われている解き方なのです。
出典:All Kids Can Learn Arithmetic(アメリカ小学校数学教師向け専門能力開発プログラム)
MOVE ITMath™(ヒューストン大学ビクトリア校,1993-2003)
NOBINOBIは、さらに
ブラッシュアップした
“チョウ分数”で
塾生さんの正答率アップに
役立てています。
図案化したオリジナル図
を使って解説していますので、
虫嫌いの皆さんにも
安心して見て頂けるはず。

分数の通分“チョウ分数”|分子が1の場合

まずは
分子が両方“1”のたし算
からです。
通分“チョウ分数”足し算(加法)
簡単な例題の計算をもとに
丁寧に解説します。
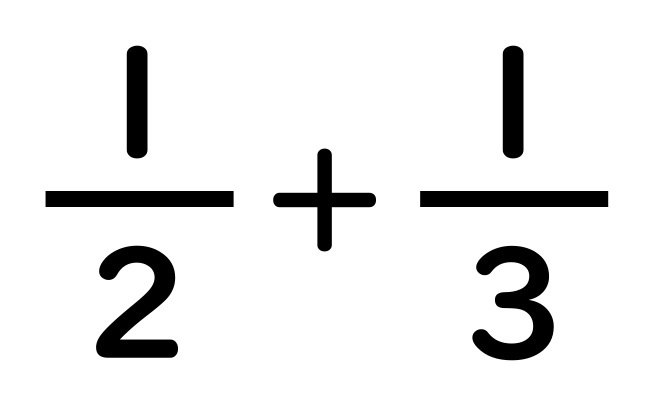
チョウ分数の解き方の手順
①分母と分母の間に、チョウのしっぽをかく。
“分母の数どうしをかける”
ことからはじめます。
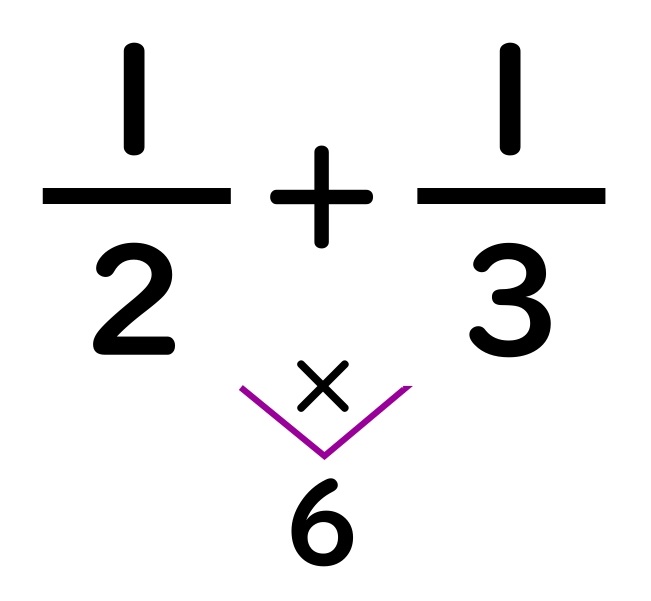
紫色のV字の部分が、
チョウのしっぽ(胴体の先端)
になります。
②ななめにちょうの羽根をかき、分子のほうに触角をかく。
分母と分子を囲むように
ななめに
チョウの羽根をかきます。
さらに、分子のほうに
チョウのしょっかくをかきます。
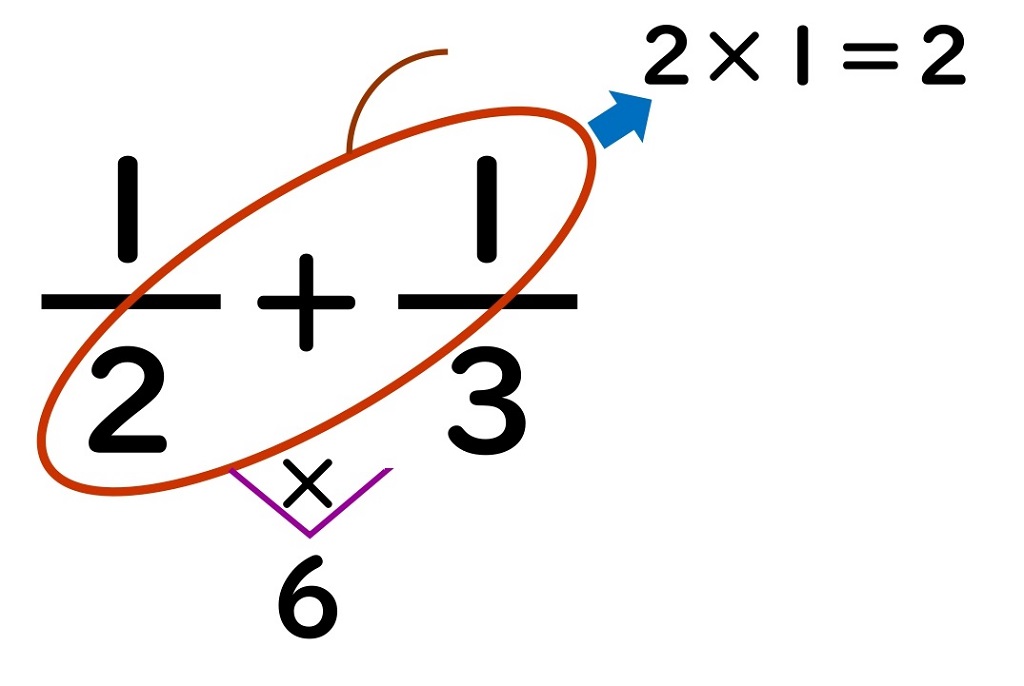
③羽根の中に入っている分母と分子をかける。
かけて出た答えは、
しょっかくの先に書きこみます。
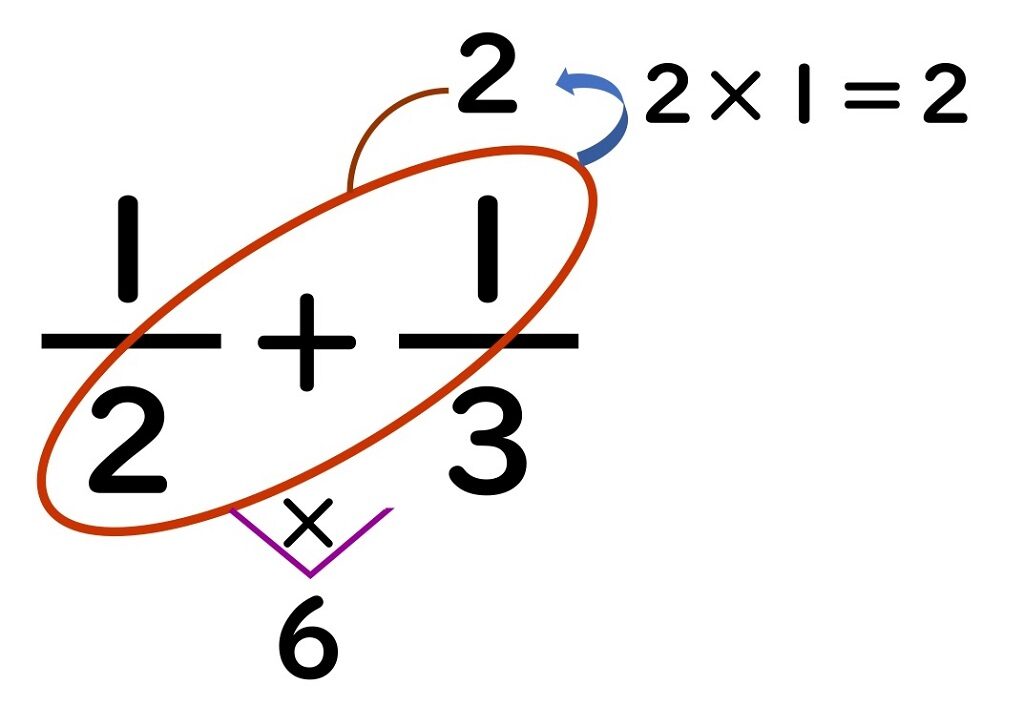
④残りも、同じように羽根をかいて、分母と分子をかける。
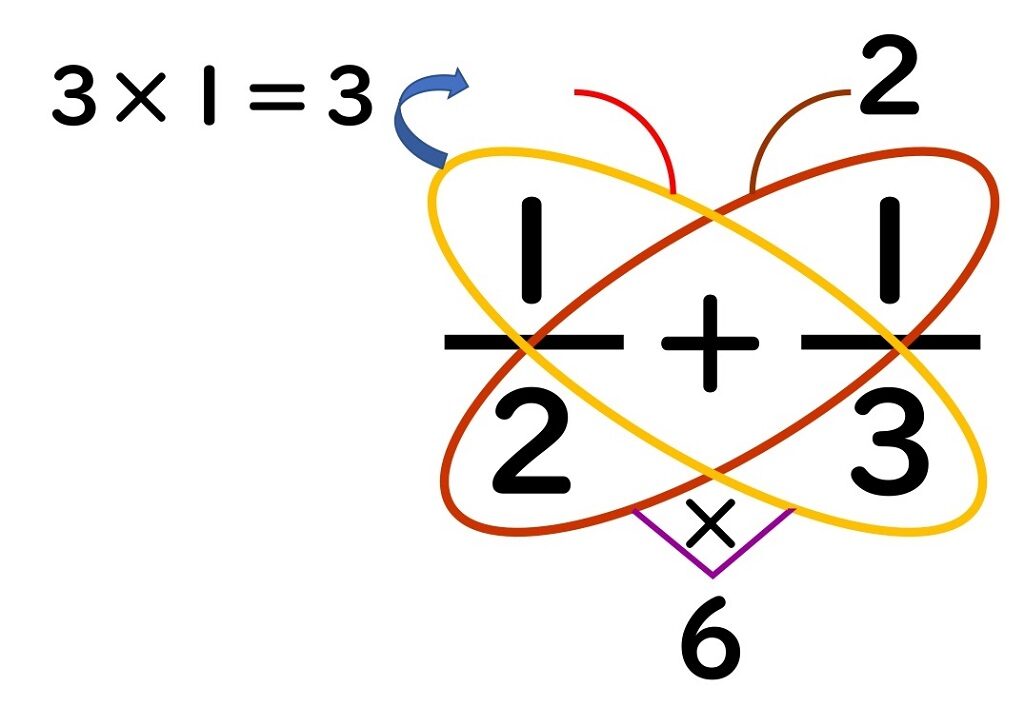
すると
こんなチョウがかけました。
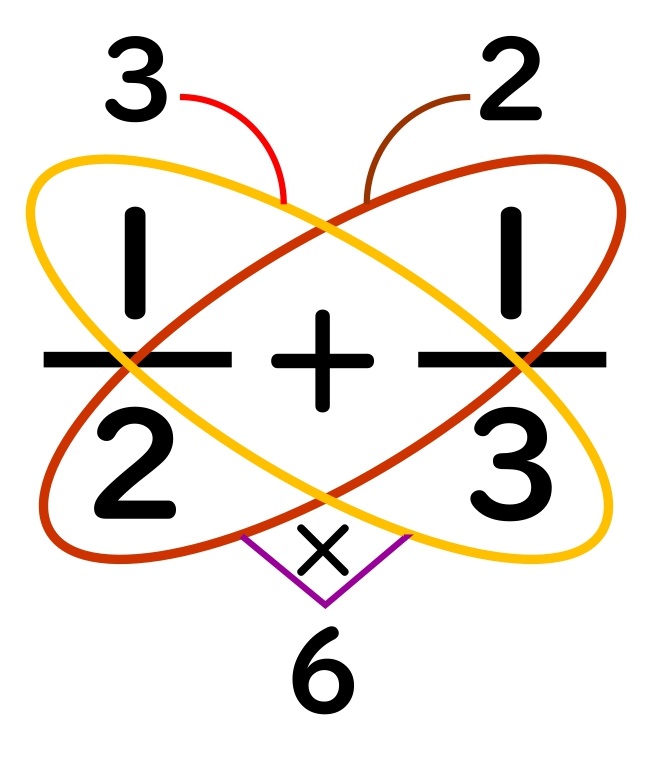
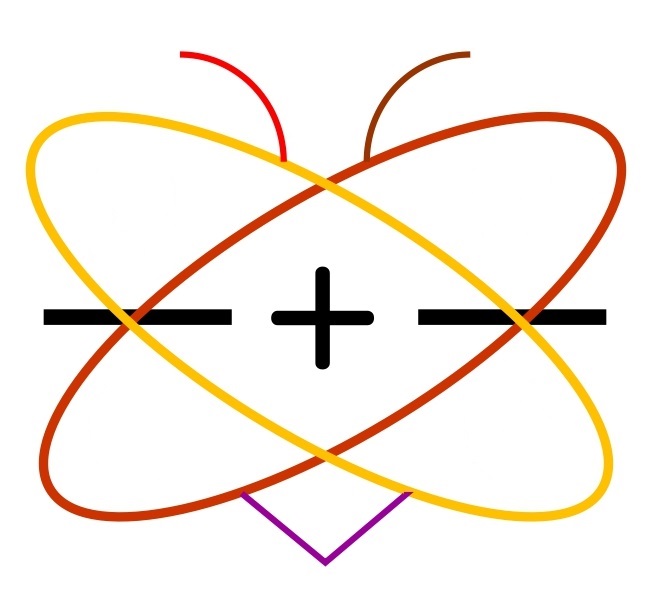
⑤数字のないチョウを描いて、計算して出した数を書きこむ。
数字のないチョウを描いて
計算して出した数を
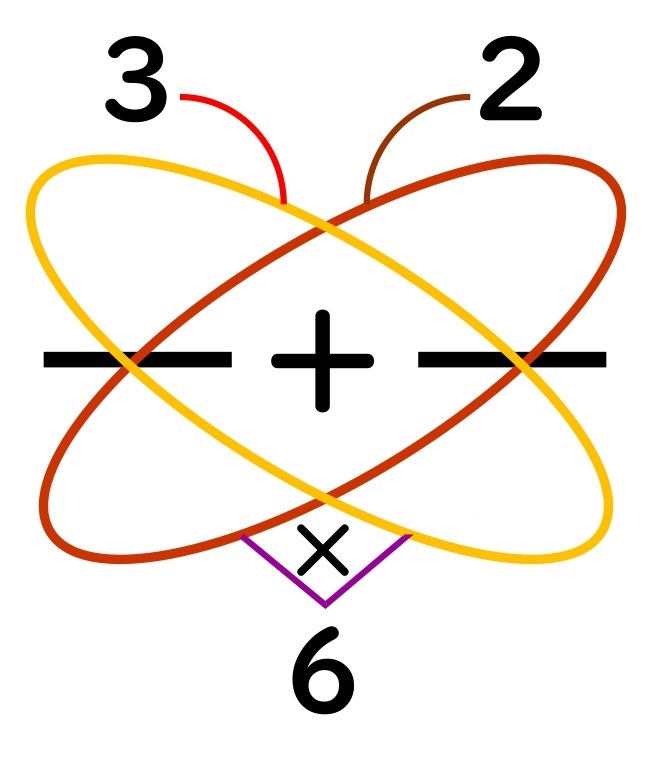
分母と分子に書きこみます。
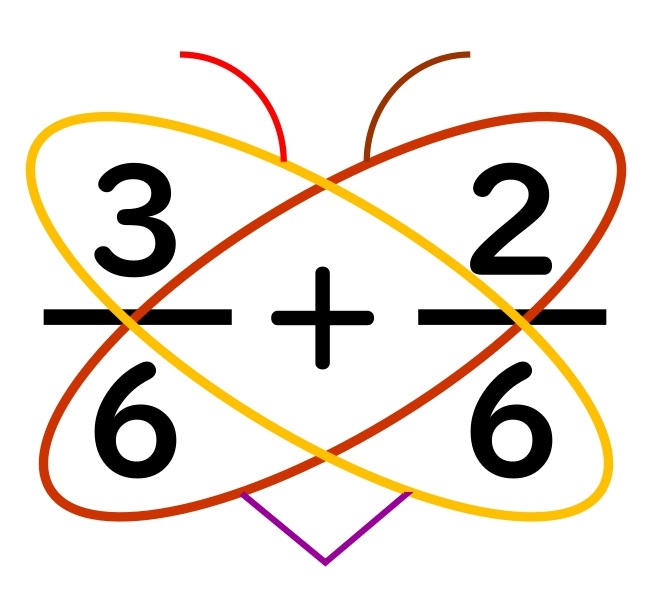
これで、元の式を
分母が同じ分数のたし算の式に
変えることができました。
面倒なときはチョウをかかず、
式だけでも大丈夫。
あとは…
⑥分子どうしをたして……完成!
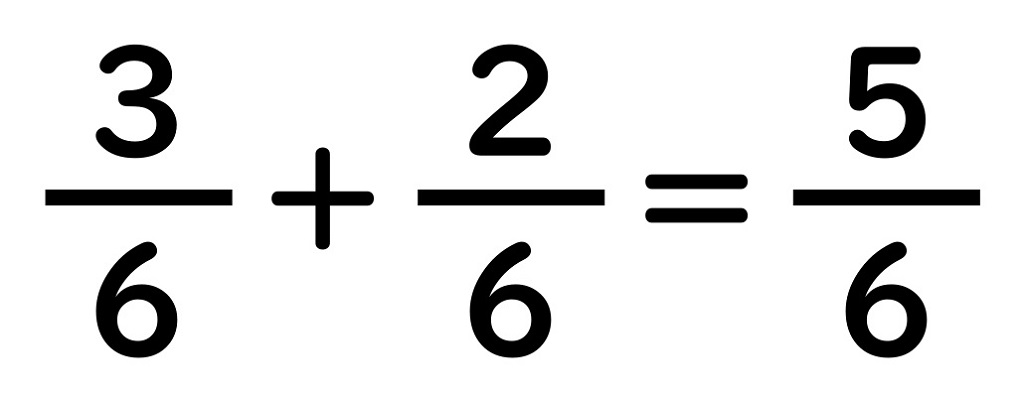
通分“チョウ分数”引き算(減法)
引き算はどうでしょうか。
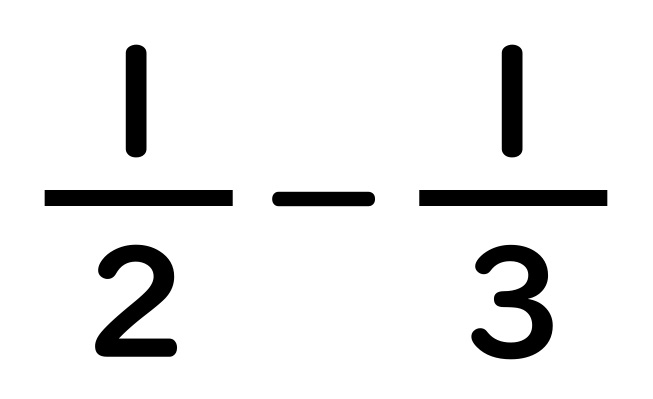
これは計算の記号を変えただけ。
計算方法は、
先ほどの足し算⑤までと全くおなじです。
計算し終わった数を
チョウに書きこむと…
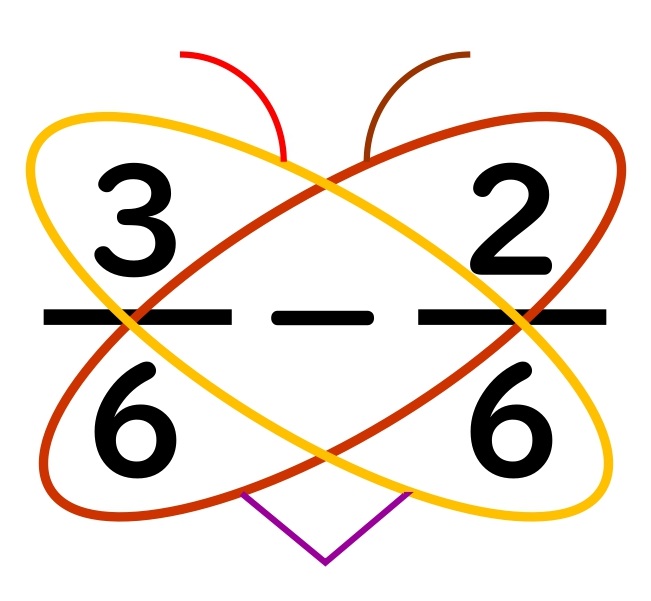

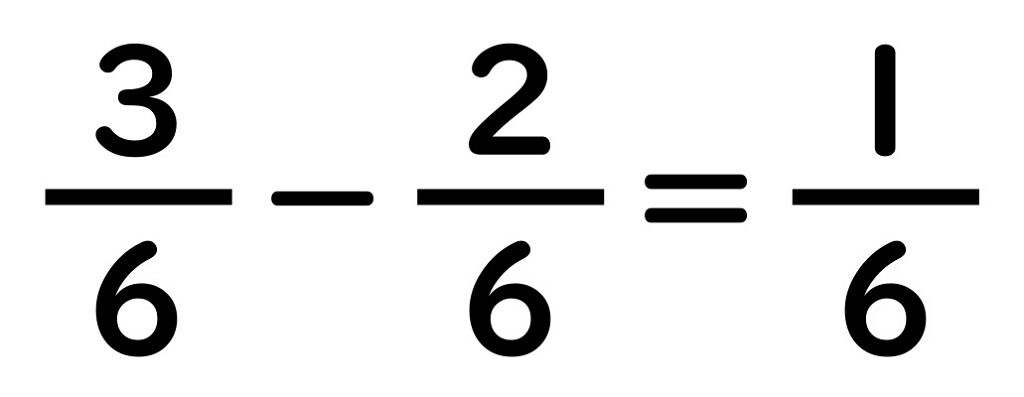
分数の通分“チョウ分数”|分子が1でない場合

分数は、分子が“1”の場合だけ
とはかぎりません。
でも、安心してください。
チョウ分数は
分子が1でなくても同じ
ように使えます。
分子が1でない場合の計算を
見ていきましょう。
通分“チョウ分数”たし算(加法)
今回も例題で見ていきます。
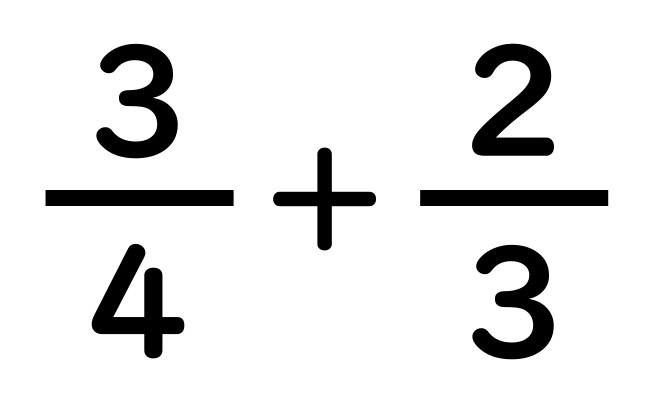
分子が1でない場合の解き方の手順
①分母と分母の間に、チョウのしっぽをかく。
分母が1の場合と同じように、分母の数どうしをかけます。
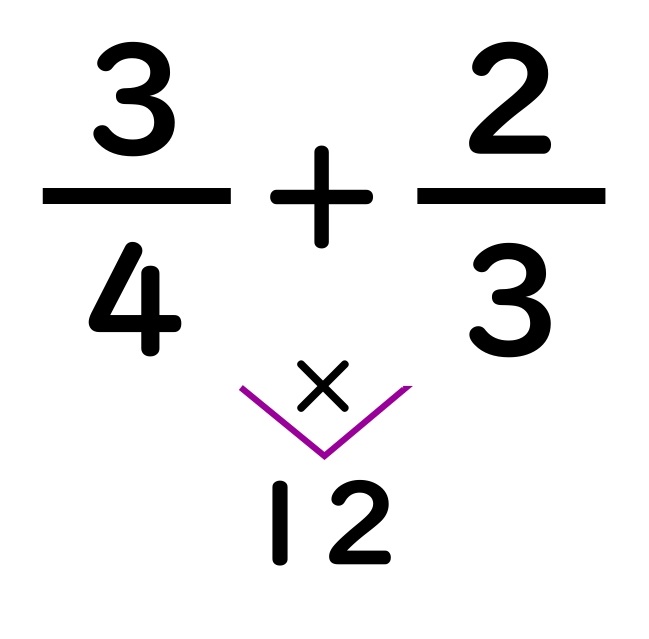
②ななめにチョウの羽根をかき、分子のほうに触角をかく。
分母と分子を囲むように
チョウの羽根を
ななめにかき、
触角をかきます。
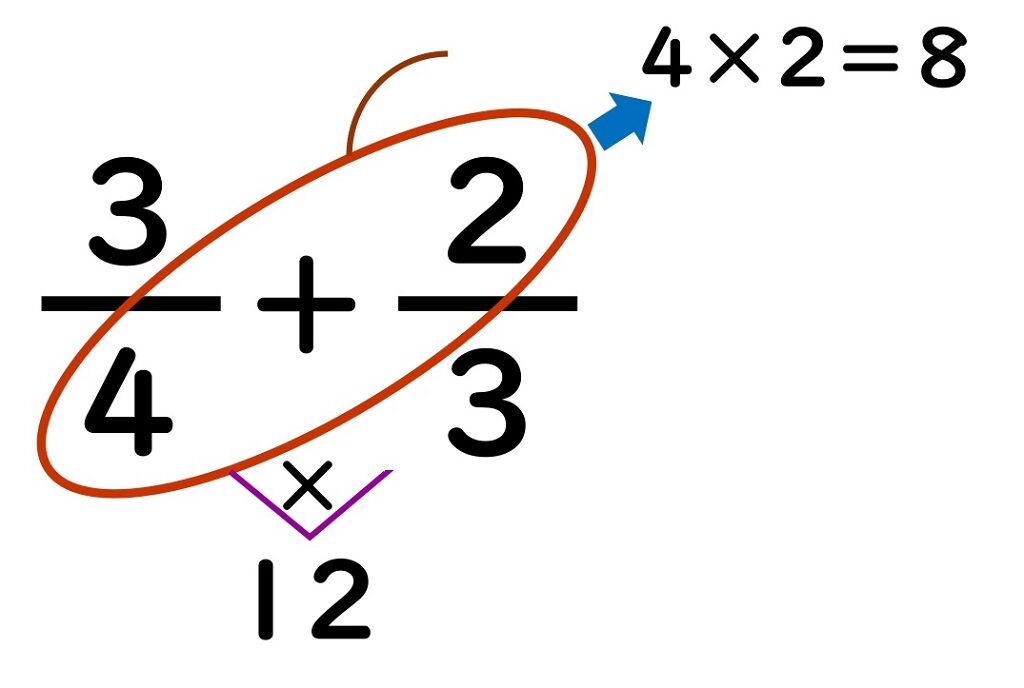
③羽根の中に入っている分母と分子をかける。
答えを触角の先に
書きいれます。
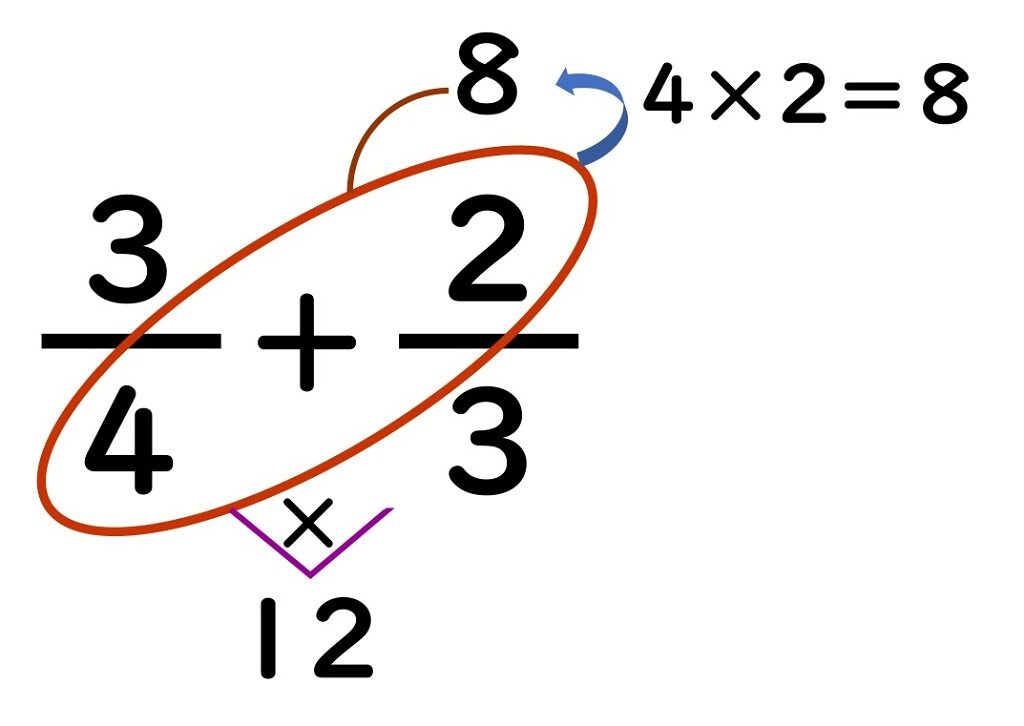
④残りも同じように羽根をかき、分母と分子をかける。
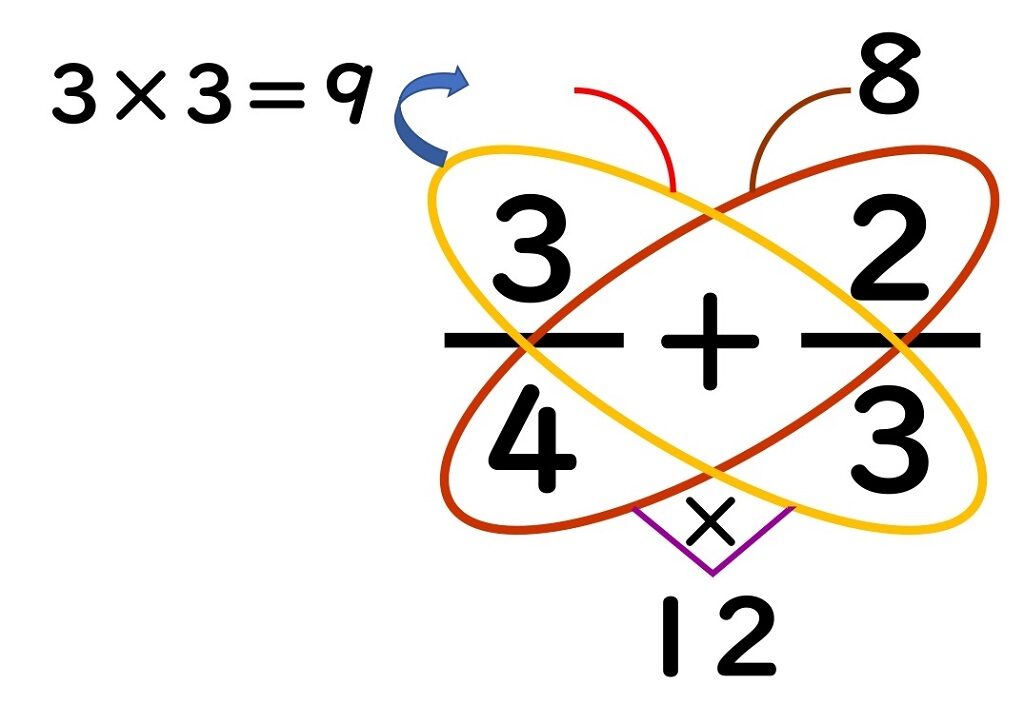
すると
こんなチョウになります。
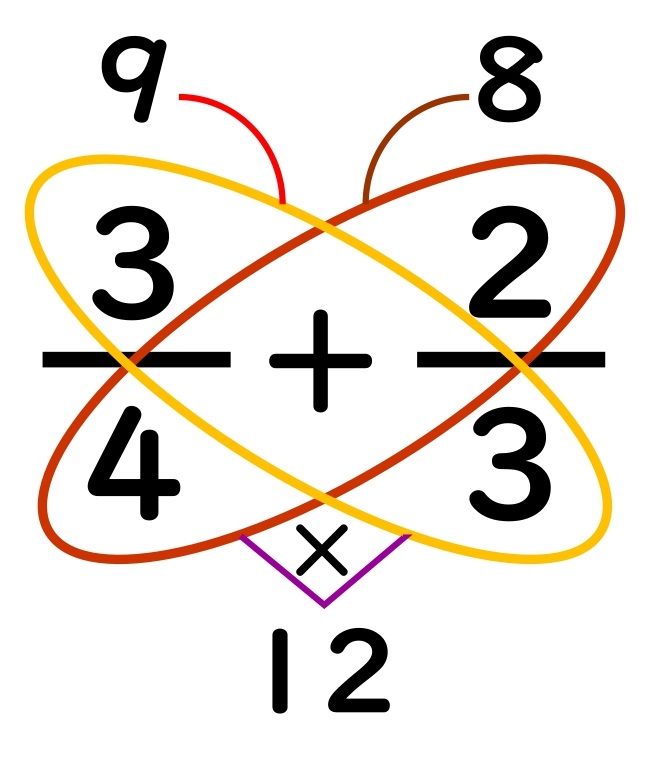
⑤もう一匹チョウをかき、計算した数を書きいれる。
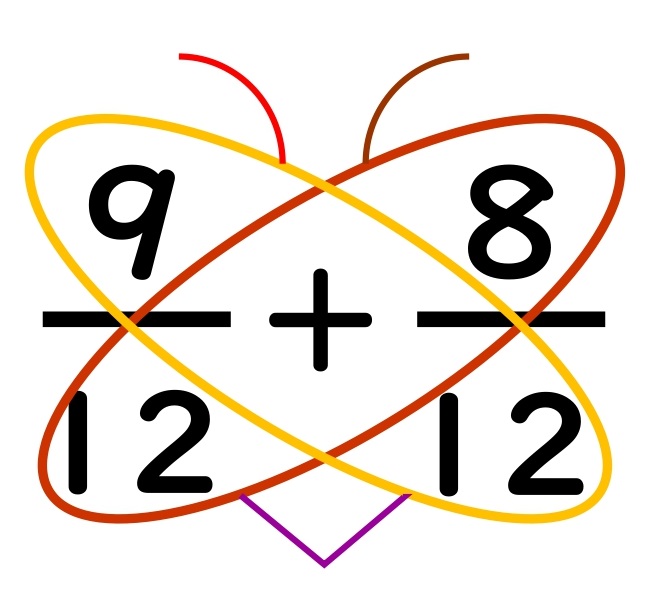
面倒なら
式だけでもOKです。
⑥分子どうしをたして、おしまい!
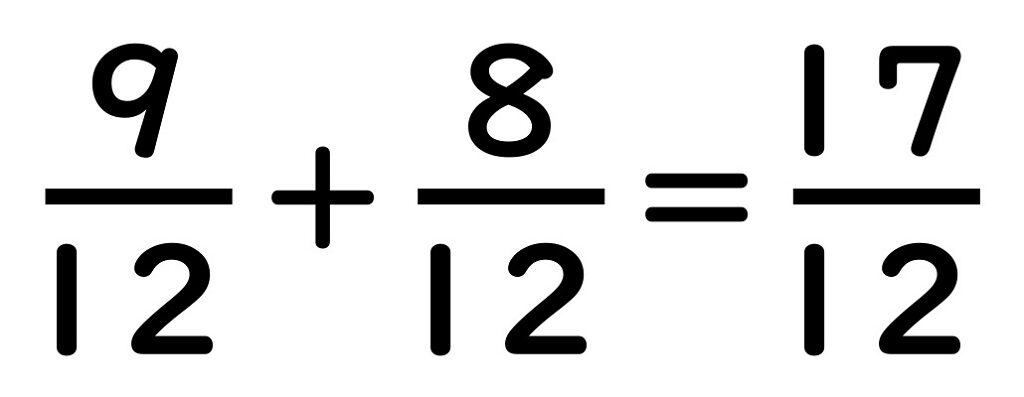
分子が分母より大きくなったら…
分子が分母より大きい分数
になりました。
これを
“仮分数(かぶんすう)”
といいます。
分母より分子が小さい分数
は
“真分数(しんぶんすう)”
といいます。
整数と真分数が
くっついている分数
を
“帯分数(たいぶんすう)”
といいます。
答えが仮分数になったときは、
帯分数になおして
みましょう。
方法は簡単。
分子の中に
分母の数が
いくつあるか?
(何セットあるか?)
確認して
整数におきかえ
ればいいのです。
まず分子の17を
“分母の数”と
“17から分母の数を引いた数”に
わけます。
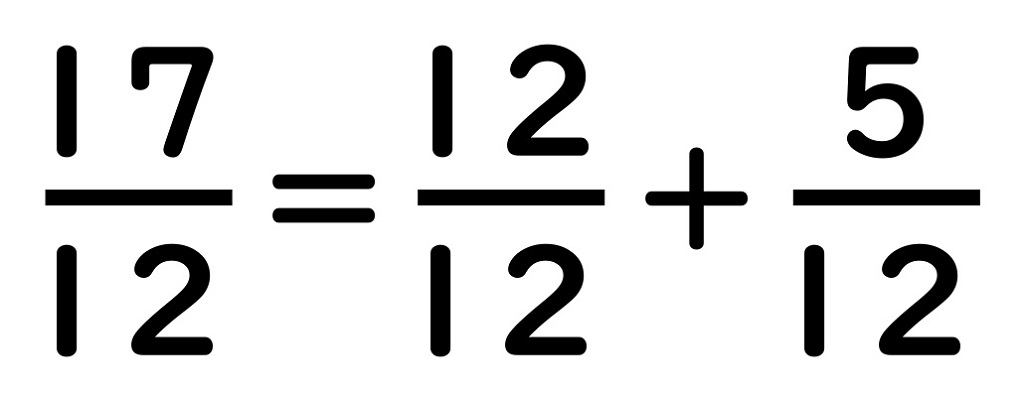
1つを12コに分けたものを、
もう一度12コぜんぶ集めれば
もとの“1つ”にもどります。
“12分の12”は“1”と同じ
なので、
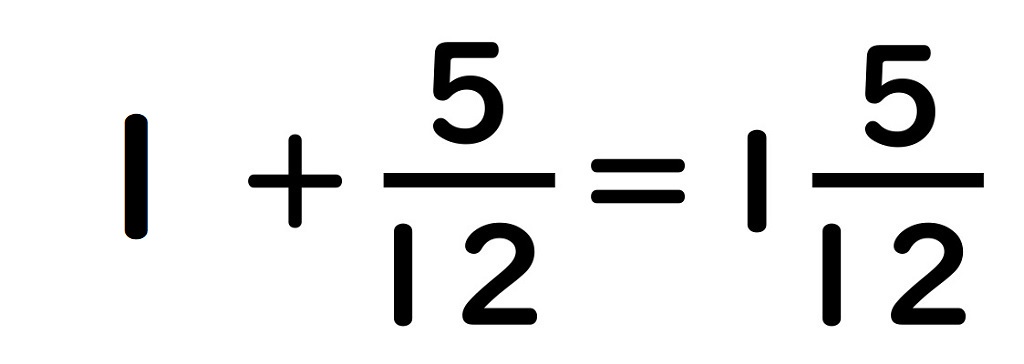
仮分数はこのように
帯分数であらわすことができる
のです。
では、ひき算はどうでしょうか?
これも分子が“1”のときと同じですので、
この例題の“たす”を“ひく”に変えて
チャレンジしてみてください。

なっているはずです!
分数の通分、計算テクニック|まとめ
 こちらの記事では、
こちらの記事では、
分数の通分が苦手な人も
正しく答えられる
計算テクニック
“チョウ分数”
を基本から説明
させて頂きました。
内容は
“バタフライ・フラクション”
=通称“ちょう分数(ちょうちょ分数)”の解説

こちらの
スライド動画でも解説していますので、ご活用ください。

ありがとうございました。
お役に立てましたら幸いです。
分数の計算を円で説明するときは、下の記事をご参照ください。
豆知識|分母分子が2ケタになったとき

分数は
分母分子が1ケタの数字だけ
とはかぎりません。
分母分子が2ケタの計算が
でてきたとき、
計算を楽にしてくれる
のが
“倍数(ばいすう)”と
“約数(やくすう)”
という考え方。
それぞれ詳しく説明すると
この記事の
文字数が多くなってしまいます。
そこで、
ここではおまけの豆知識として
簡単に解説します。
倍数(ばいすう)
ある整数に整数をかけた数を
ある整数の倍数(ばいすう)
といいます。
たとえば、整数“3”に
整数“1”、“2”、“3”を
それぞれかけると、
“3”、“6”、“9”になります。
この“3”、“6”、“9”それぞれが
整数“3”の倍数です。
日常生活では
3の1倍、2倍、3倍
と呼んでいます。
また
2つ以上の整数に共通する倍数を
“公倍数(こうばいすう)”
といいます。
公倍数の中で一番小さいものが
最小公倍数
(さいしょうこうばいすう)。
公倍数は、すべて
最小公倍数の倍数
になります。
2ケタ以上の分母をもつ
2つの分数を通分して
計算するとき
最小公倍数をさがすことで、
数を小さくすることができ、
計算しやすくなるのです。
約数(やくすう)
ある整数を
割りきることができる整数のことを
約数
(やくすう)といいます。
2つ以上の整数に共通な約数を
それらの整数の
公約数
(こうやくすう)
といいます。
公約数の中で一番大きいものが
最大公約数
(さいだいこうやくすう)。
公約数はすべて
最大公約数の約数
です。
公約数は、
分母と分子が2ケタの分数を
簡単な分数に変えるとき
や
最小公倍数をみつけだすとき
に使います。














