
中学数学の基本「一次方程式」。
方程式の「利用」や「応用」というかたちで、文章問題が出題される単元でもあります。
別の記事でご紹介した通り、文章問題は主に8種類。
新潟市のマンツーマン個別指導塾スクールNOBINOBIのサイトに初めて訪問してくださった皆様へ「良く出題される順」をご紹介すると、
②代金・個数に関する問題
③過不足に関する問題
④年齢・分配・貯金に関する問題
⑤自然数・整数に関する問題
⑥割合に関する問題
⑦図形に関する問題
⑧平均に関する問題
となります。
当塾の塾生さんたちには、とくに良く出題される
①道のり・速さ・時間に関する問題
の解説に力を入れていますが、出題パターンが多く

な生徒さんたちもいます。
そこでこちらの記事では単元「一次方程式の利用」の「道のり・速さ・時間」の基本の問題を取りあげます。
- 記事の内容は、
「おいつく」「まわる」「かわる」の3つ。
●「おいつく」問題の解き方
解き方の手順にそって解説。
●まとめ
となっています。
この記事を書いているのは、

●開校5年半で、新潟県内トップ私立高校合格者を輩出。
●年評定平均:中学時代3.7→高校進学後4.9、4.8の塾生を輩出。
●サポートした不登校の卒塾生、大学へ進学。
●当ブログ、にほんブログ村カテゴリー「中学受験(個人塾)」
で、2020年6月から13ヶ月連続ランキング1位。
2020年3月開設15ヵ月目で月間4万PV超達成。
●元公立高校教員
●現役カウンセラー
こと“のびのび”です。

「道のり・速さ・時間」の主な出題タイプ3つ

「道のり・速さ・時間」の問題には多くの種類があります。
その中でも代表的な問題は
先に出発した人に後から追いかける人が「おいつく」タイプ、
二人がグランドや池などの周囲を「まわる」タイプ、
途中で速さや手段が変化する「かわる」タイプの3タイプ。
ここでは「おいつく」タイプの例題について、解きながら解説していきます。
苦手な人向けに基本的な考え方を理解してもらうための内容ですので、

という人は、どんどん飛ばして読み進めてください。


「おいつく」問題の解き方

ここでは例題を、解き方の手順にそって解きながら解説していきます。
一次方程式の利用文章問題「おいつく」の例題
ユキさんの忘れ物に気づいたお姉さんのサキさん。
忘れ物を届けるためサキさんが自転車で家を出発したのは、ユキさんが出発してから18分後。
同じ道を追いかけました。
ユキさんは分速50m、サキさんは分速200mでそれぞれ一定の速さで進むとすると、
サキさんが家を出発してから何分後に追いつくでしょうか。
一次方程式文章問題の解き方は、
② 条件をすべて書きだす。
③ 解りにくいときは、絵や図を描いてみる。
④ 求めるものをx(エックス)におきかえる。
⑤ 「=(イコール)」の左側と右側が同じになるように式をつくる。
ユキさん:毎分50mですすむ。
サキさん:ユキさんが出発して18分後
毎分200mですすむ。
サキさんが家を出てユキさんに追いつくのは何分後?
となります。
ニガテな人はこれだけでは解きにくいと思います。
③解りにくいときは、絵や図を描いてみるとグッとわかりやすくなります。
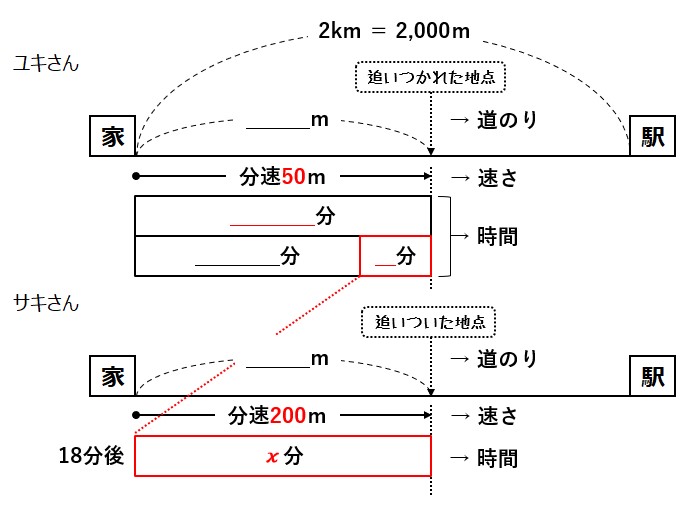
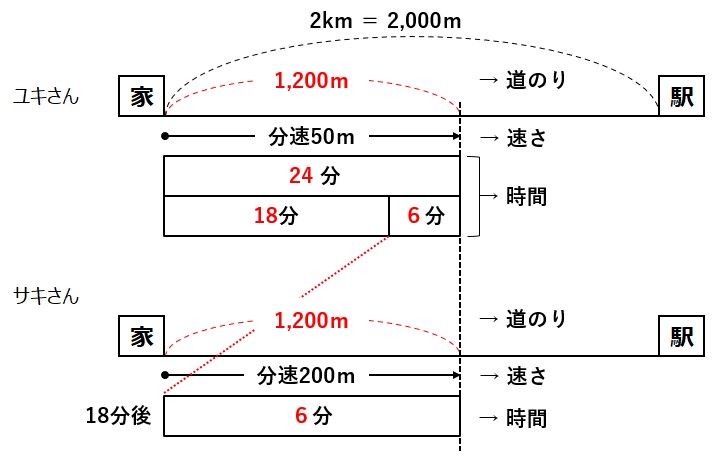
図は「二人が進んだ道のり(距離)は同じ」ことに注目して描いています。
④求めるものをxとすると…
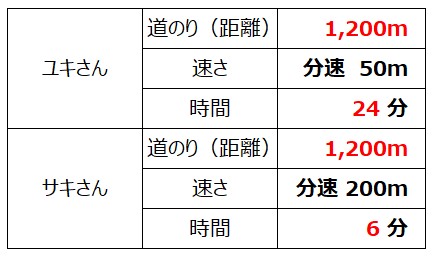
図に書き込んでもわかりにくい場合は、②で挙げた道のり(距離)、速さ、時間の条件を表にしてみるのも良い方法です。
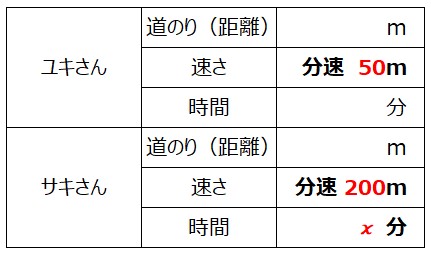
何がわかっていて何がわからないのか、ハッキリしたのではないでしょうか。
図や表をもとに、方程式をつくっていきましょう。
方程式は⑤「=(イコール)」の左側と右側が同じになるように式をつくるようにします。
ユキさんとサキさんの進んだ距離=道のりは同じはずです。
図や表から、サキさんの道のりはすぐ表せそうです。
で1分ですすむ道のりは200mですので、
サキさんの道のり= 200m × x 分
= 200x
となります。
一方、ユキさんの道のりはどうでしょう。
ユキさんはサキさんが家を出る前に、18分歩いて進んでいました。
その地点からさらに「サキさんが自転車で走った時間」と同じ時間歩いています。
ですので、
ユキさんの道のり= 50 m × 18分 + 50 m × x 分
ユキさんのスピードは一定で変わりませんので、式をまとめると
50 m × 18分 + 50 m × x 分
= 50 m/分×( 18分 + x 分 )
= 50 ×( 18 + x )
図と表にあてはめると、
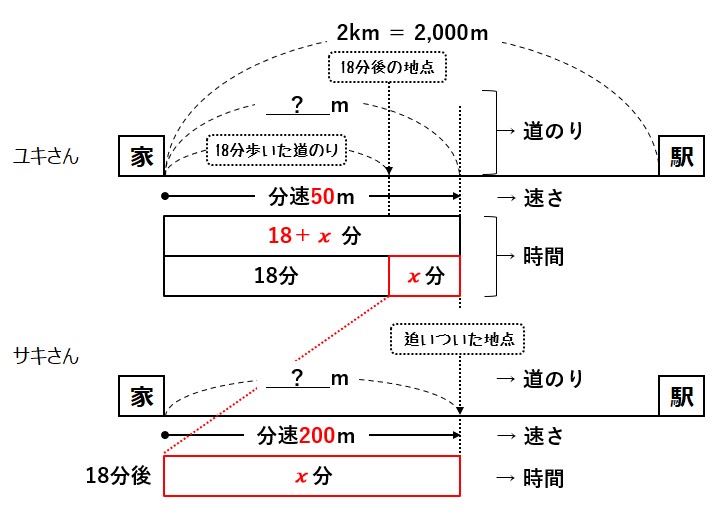
サキさんの道のり=ユキさんの道のり(図表中の「?」)のはずですから、
となります。

あとは、この式を解けば、サキさんがかかった時間 x をもとめることができます。
200x = 50 ( 18 + x )
( )を外すには「50」を「18」、「x 」それぞれにかけます。
200x = 900 + 50 x
+50 x を=の左がわにもっていって
200 x - 50 x = 900
150 x = 900
最後に「=」の両側を150でわれば、 x がもとめられます。
150 x ÷ 150 = 900 ÷ 150
x = 6
ことがわかりました。
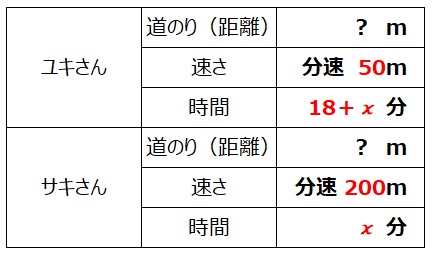
答えをもとに、すべて計算して図表に入れてみると、
このようになります。

まとめ

こちらの記事では単元「一次方程式の利用」の「道のり・速さ・時間」の基本の問題を取りあげて解説してきました。
記事の内容は、
●「道のり・速さ・時間」の主な出題タイプは
「おいつく」「まわる」「かわる」の3つ。
●「おいつく」問題の解き方
解き方の手順にそって解説。
●まとめ
一次方程式文章問題の解き方
② 条件をすべて書きだす。
③ 解りにくいときは、絵や図を描いてみる。
④ 求めるものをx(エックス)におきかえる。
⑤ 「=(イコール)」の左側と右側が同じになるように式をつくる。

ここで取り上げた問題の解き方を参考に、数学の実力アップにつなげて頂ければ幸いです。
一次方程式の文章問題、
理科ででてくる「濃度」の基本を合せて説明している以下の記事もご参照ください。

少しでも皆さんのお役に立てれば幸いです。

















