中学の数学ででてくる方程式の基本「一次方程式」。
「利用」や「応用」といった単元名で、文章問題を学習します。
別の記事でご紹介した通り、文章問題は主に8種類。
初めて訪問してくれた生徒さんのために「良く出題される順」にあげると、
②代金・個数に関する問題
③過不足に関する問題
④年齢・分配・貯金に関する問題
⑤自然数・整数に関する問題
⑥割合に関する問題
⑦図形に関する問題
⑧平均に関する問題
となります。
新潟市で運営中の個別指導塾には、⑥割合に関する問題
なかでも特に

な生徒さんたち、かなりいます。
そこでこちらの記事では、中学数学「一次方程式の利用」の文章題⑥「割合の問題」のうち「濃度の問題」をピックアップ!
- 記事の内容は、
●「一次方程式の解き方の手順」5つのポイント(おさらい)
●「濃度の問題」解き方その1「うすめる」場合
●「濃度の問題」解き方その2「こくする」場合
●「濃度の問題」解き方その3「まぜる」場合
●まとめ
●豆知識:濃度の計算、基本をおさらい
となっています。
この記事を書いているのは、

現役プロ講師&経営者
●現役カウンセラー
●元公立高校教員

目次【タップでジャンプ】
「濃度の問題」、解き方の手順

中学の数学でとりあげられる濃度の文章問題は、一次方程式をつかうと楽に答えを導きだすことができます。
解き方の手順は、
② 条件をすべて書きだす。
③ 解りにくいときは、絵や図を描いてみる。
④ 求めるものをx(エックス)におきかえる。
⑤ 「=(イコール)」の左側と右側が同じになるように式をつくる。
この手順にそって、良く出る
「うすめる」、「こくする」、「混ぜる」の3つの例題
をひとつずつ解説していきます。
その前に、一次方程式の基本と理科の濃度の基本をおさえたい!という人は、こちらの記事をご参照ください。
[sitecard subtitle=関連記事 url=https://school-nobinobi.com/application-problems-of-linear-equations-for-concentration/ target=self]
例題1:濃度をうすめる

問:5%の塩水を4%にするには?
5%の塩水が300gある。

水を何g加えればいい?
問題をとくときの手順にそってみていきましょう。
① 文章を小分けにして読む。→ 読んでもらったと思います(^^)
② 条件をすべて書きだします。
5%の塩水:300g
4%の塩水にする
水を何g加える?
③ 解りにくいときは、絵や図を描いてみるのも良い方法です。
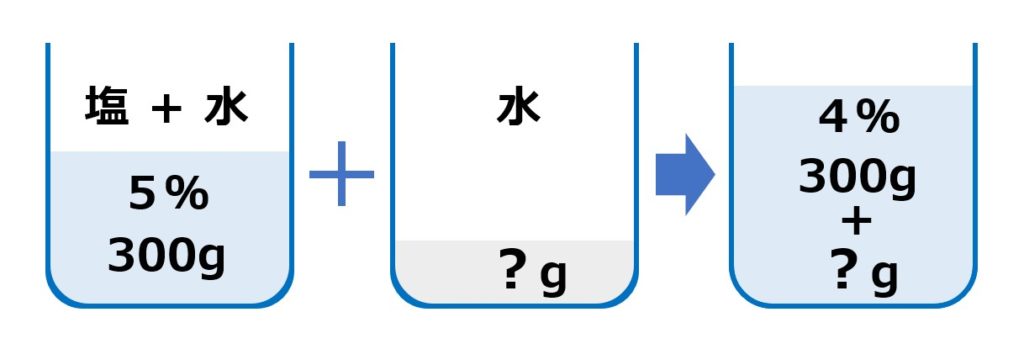

そこで、④求めるもの(加える水)をx(エックス)におきかえます。
「 加える水 = x 」として、
⑤「=(イコール)」の左側と右側が同じになるように式をつくります。
ポイントは、
●塩水に入っている塩の重さ(量)は、うすめる前もうすめた後も変わらない。
●塩の重さは、うすめる前の塩水から計算でだせる。
※塩の重さの出し方は、この記事一番下の
「豆知識コーナー」で確認できます。
●「 うすめる前 = うすめた後 」になるように方程式をつくる。
100倍してパーセントにしています。
塩水を作る前にもどすためにパーセントをそれぞれ100でわるので…
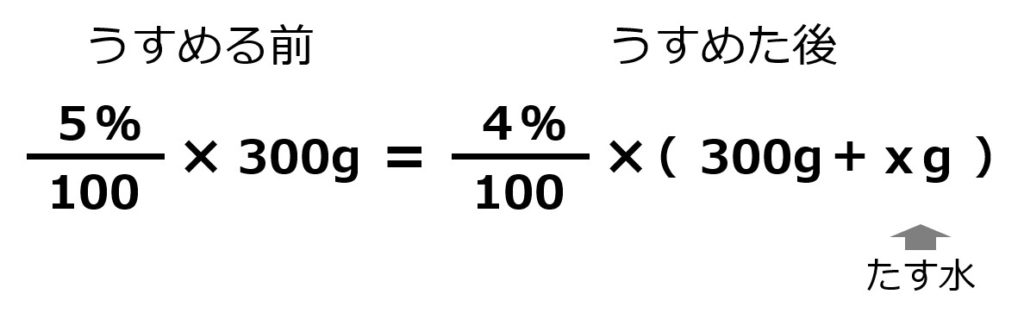
1 / 20 × 300 = 1 / 25 × ( 300 + x )
15 = 300 / 25 + x / 25
ポイントでお話したとおり、「=」の左がわの計算から
この塩水には塩が15g入っている
ことがわかります。
「=」の左がわと右がわ両方に25をかけて
375 = 300 + x
x = 375 - 300
x = 75
加える水の重さをxとしましたので
75gの水を加えると、4%にうすめられる
のです。
例題2:濃度をこくする

問:3%の砂糖水を4%にするには?
今度は、逆に濃度を濃くする例題。
塩水を砂糖水に変えてみます。
3%の砂糖水が240gある。

砂糖を何g加えればいい?
例題1と同じように問題をとく手順にそってみていきましょう。
① 文章を小分けにして読む。→ 読んでもらったということでいいですよね(^^)
② 条件をすべて書きだします。
3%の砂糖水:240g
4%の砂糖水にする
砂糖を何g加える?
③ 解りにくいときは、絵や図を描いてみるのも良い方法です。
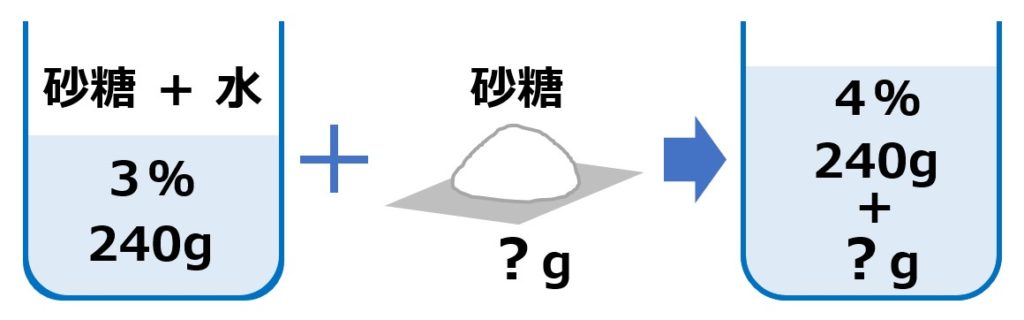

そこで、④求めるもの(加える砂糖)をx(エックス)におきかえます。
「 砂糖 = x 」として、
⑤「=(イコール)」の左側と右側が同じになるように式をつくります。
ポイントは、
●3%の砂糖水の砂糖の重さと加える砂糖の重さの合計が、4%の砂糖水の砂糖の重さと同じ。
●「加えた砂糖の重さ分、砂糖水全体も重くなる」点に気をつけて!
100倍してパーセントにしています。
砂糖水を作る前にもどすためにパーセントをそれぞれ100でわるので…

720 / 100 + xg = 1 / 25 ×( 240g + xg )
「=」の左辺と右辺に25をかけて
25 × ( 7.2 + x )= 240 + x
180 + 25x = 240 + x
24x = 240 - 180
24x = 60
x = 2.5
xは加える砂糖の重さでしたので、
もとの砂糖水に
2.5gの砂糖を加えると、4%の濃さになる
ことがわかりました。
例題3:混ぜて濃さを変える

問:5%の砂糖水と8%の砂糖水を混ぜて7%にするには?
最後は、2つの水溶液を混ぜて、濃さを変える問題。
ここでも砂糖水を使ってみます。
5%の砂糖水と8%の砂糖水を混ぜて、7%の砂糖水を240gつくりたい。

これまでと同じように問題をとく手順にそってみていきましょう。
① 文章を小分けにして読む。→ 読んでもらったと信じています(^^)
② 条件をすべて書きだします。
5%の砂糖水+8%の砂糖水
7%の砂糖水を240g
5%の砂糖水は何g?
③ 解りにくいときは、絵や図を描いてみると良いんでした。
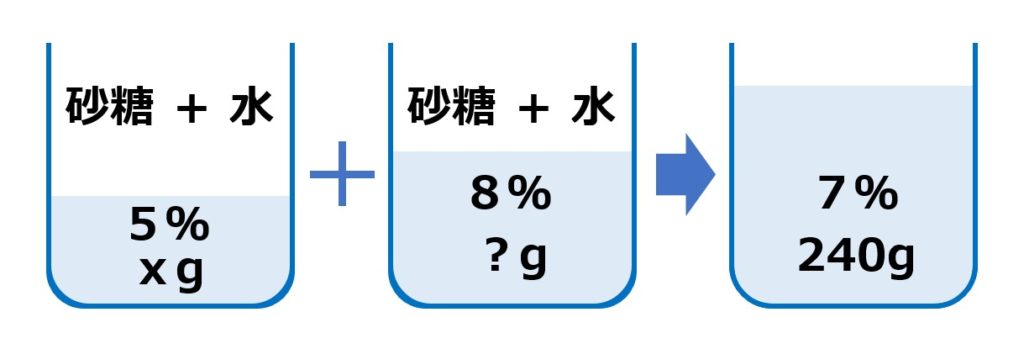

そこで、④求めるもの(5%の砂糖水)をx(エックス)におきかえます。
「 5%の砂糖水 = x 」として、
⑤「=(イコール)」の左側と右側が同じになるように式をつくります。
ポイントは、
●5%の砂糖水の砂糖の重さと8%の砂糖水の砂糖の重さの合計が、7%の砂糖水の砂糖の重さと同じ。
●5%の砂糖水をxgとすると、8%の砂糖水の重さ「?」はxを使ってどう表したらいい?
これさえわかれば、あとはこれまでと同じ!
100倍してパーセントにしています。
砂糖水を作る前にもどすためにパーセントをそれぞれ100でわるので…
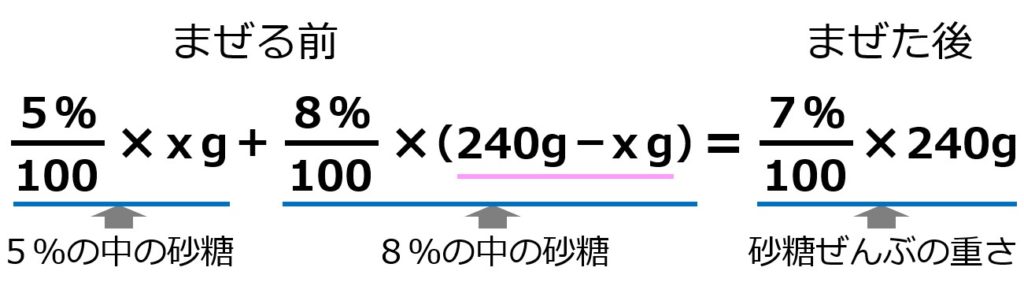
両辺に100をかけて、
5x + 8 ×( 240 - x ) = 7 × 240
5x + 1920 - 8x = 1680
-3x = 1680 - 1920
-3x = -240
x = 80
5%の砂糖水がxgでしたので、
5%の砂糖水80gと8%の砂糖水160g(240 - 80)をまぜれば、
7%の砂糖水が240gできるのです。
まとめ

こちらの記事では、中学数学「一次方程式の利用」の文章題⑥「割合の問題」のうち「濃度の問題」の解き方を3つの例題で解説してきました。
記事の内容は、
●「一次方程式の解き方の手順」5つのポイント(おさらい)
●「濃度の問題」解き方その1「うすめる」場合
●「濃度の問題」解き方その2「こくする」場合
●「濃度の問題」解き方その3「まぜる」場合
となっています。
ここで取り上げた濃度の問題の解き方を参考に、
数学と理科両方の実力アップにつなげて頂ければ幸いです。
理科ででてくる「濃度」の基本を合せて説明している以下の記事もご参照ください。
[sitecard subtitle=関連記事 url=https://school-nobinobi.com/application-problems-of-linear-equations-for-concentration/ target=self]

最後に「豆知識:濃度の計算の基本」も掲載!
皆さんのお役に立てれば幸いです。
濃度の計算 基本を使ってみよう!
次に、濃度に関する計算方法をみてみましょう。
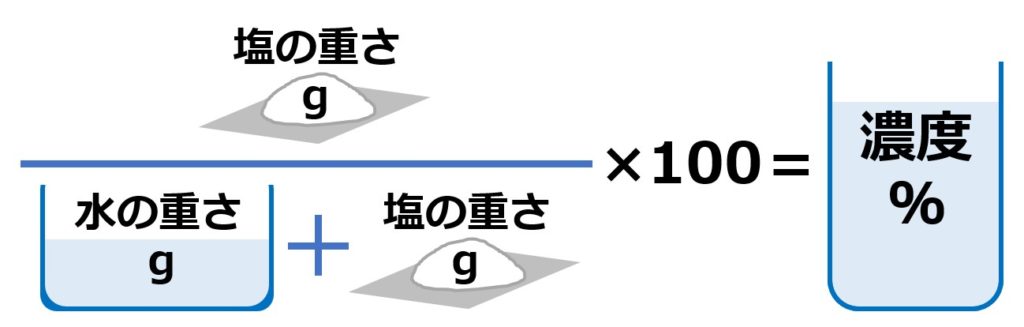
濃度(パーセント)と重さ(質量=グラム=g)がわかる塩水があって、

と、聞かれたら…
濃度(%)は、100倍してパーセントにしていますから、
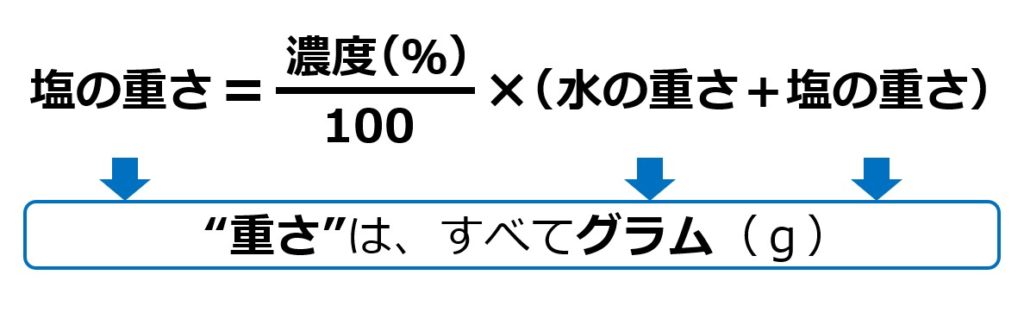
①まず濃度を100でわる
②でた数に、塩水全体の重さ(単位はg)をかける
ことで、塩の重さ(g)を出すことができるのです。
【関連ページ】当スクールの取り組みにつきましては、下記ページをご参照ください。