
皆さんは、“立方体”と聞くと何をイメージされますか?


そうなんです!
正方形だけでかこまれたかたち
のことを立方体といいます。
こちらの記事では、
“立方体”と“展開図”について、
苦手な生徒さんでも
簡単に理解できるよう
パターンを解説。
立方体の
頂点(かど)や
展開図の点の
基本問題の解き方も
あわせて説明
していきます。
- 記事の内容は
●立方体の展開図、苦手な人は4つのパターンで理解
●立方体の展開図、鏡にうつしても、回転しても、同じパターン
●これで完璧!“立方体の頂点”“展開図の点”の問題の解き方を例題で解説。
●まとめ
●豆知識|立方体の展開図、重なる2点の見つけ方

●小中学生対象完全個別指導塾の校長(経営者兼専任講師)
●開校5年半で、新潟県内トップ私立高校合格者を輩出。
●年評定平均:中学時代3点台→高校進学後4.9、4.8、4.4の塾生を輩出。
●サポートした不登校の卒塾生、大学へ進学(卒業)。
●オリジナル直筆記事、グーグル3ワード検索で1位(2024.4.1現在)
●当ブログ、にほんブログ村カテゴリー「中学受験(個人塾)」
で、2020年6月から36ヶ月以上連続ランキング1位。
2020年3月開設15ヵ月目で月間4万PV超。
●元公立高校教員
●現役カウンセラー

オリジナルイラスト付き!

目次【タップでジャンプ】
立方体と展開図の基本

立方体(りっぽうたい)の基本
立方体は“正六面体”とも呼ばれる立体。
正六面体(せいろくめんたい、英: regular hexahedron)または立方体(りっぽうたい、英: cube)とは、正多面体の一種であり、空間を正方形6枚で囲んだ立体
「6枚の正方形でできた箱」は、直方体(六面体、直六面体、長方体)の仲間。
小学校4年生の算数で勉強する、立体の基本です。
見取図(投影図)は、
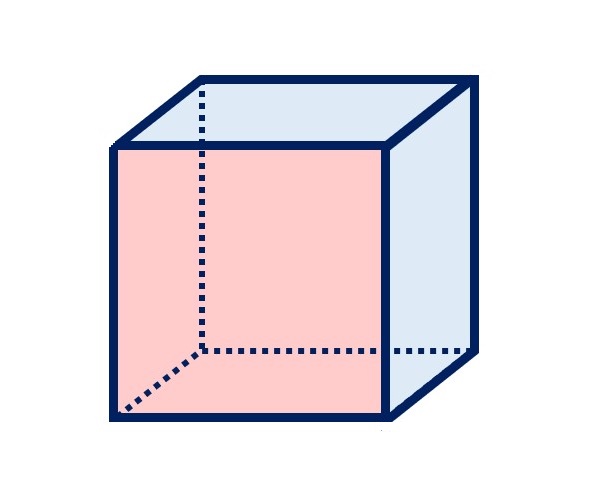
で、点線は、立方体の実物を見た時かくれて見えない辺をあらわしています。
各部分の名前は、
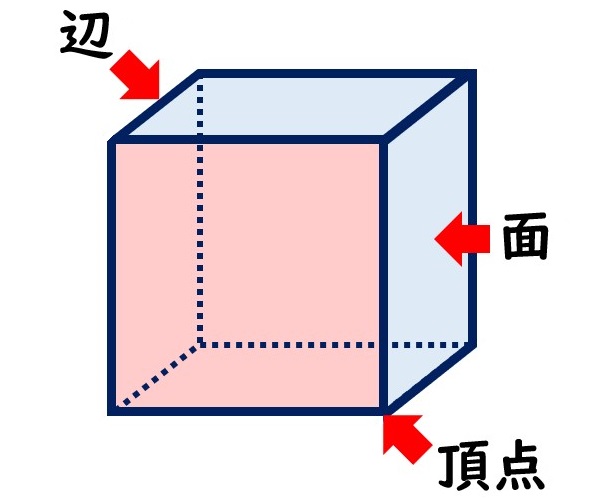
立方体の特徴は、
●6つの面は、全て正方形。
●6つの面の角は、全て直角(90度)。
●頂点は8つ。
●辺は全て同じ長さ。本数は12本。
展開(てんかい)の基本
展開とは、
と言いかえることができます。
ではさっそく、先ほどの立方体の紙箱をハサミで切って展開してみましょう!
展開の一例
①はじめに赤い矢印の3つの辺を切ります。
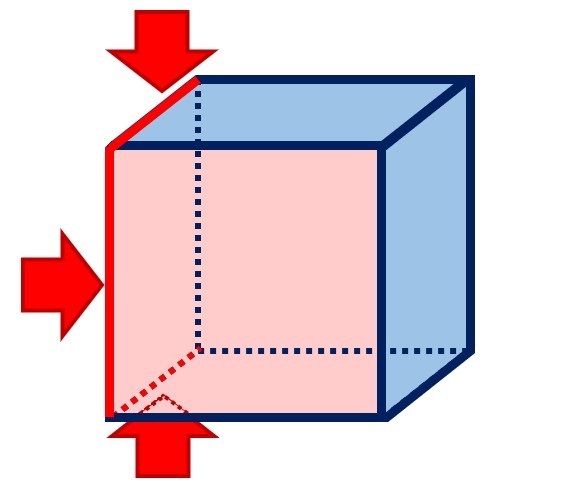
辺を切った“面”を赤い点線の矢印にそって広げます。
ぱかっ!
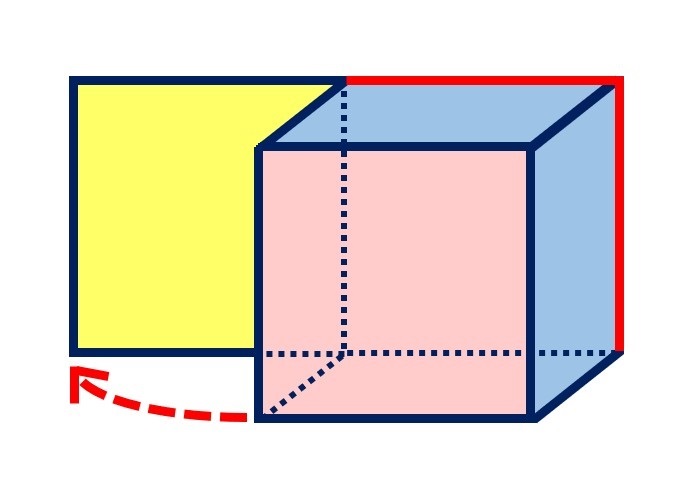
②上の図の、赤い2つの辺を切って、むこう側に広げます。
ぱかかっ!
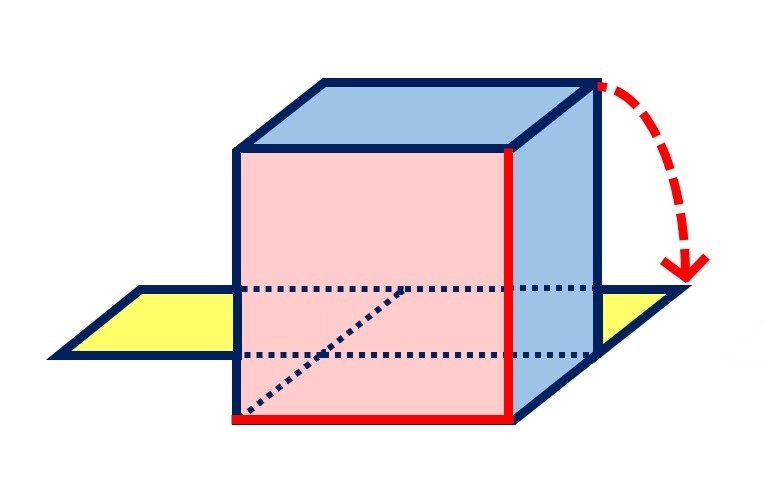
③上の図の、赤い2つの辺を切って、上に持ち上げます。
よいしょ!
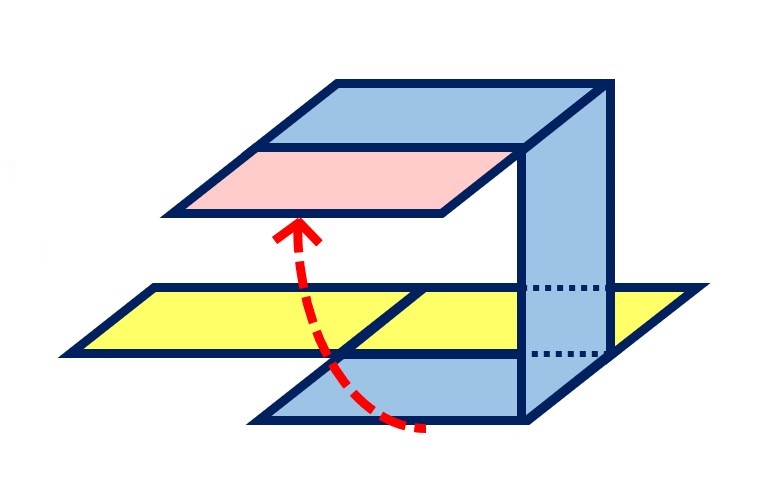
④立っている1つの面を、右にたおして広げます。
ぱたん!
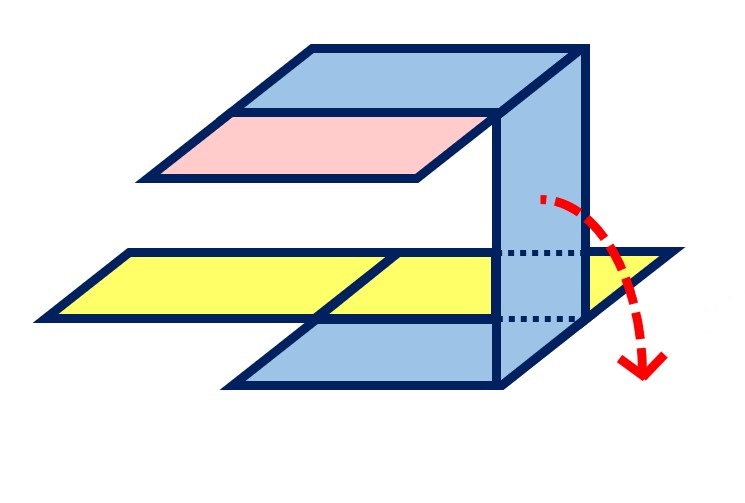
⑤立っている2つの面を、両方いっしょに右にたおして広げます。
ぱたたん!
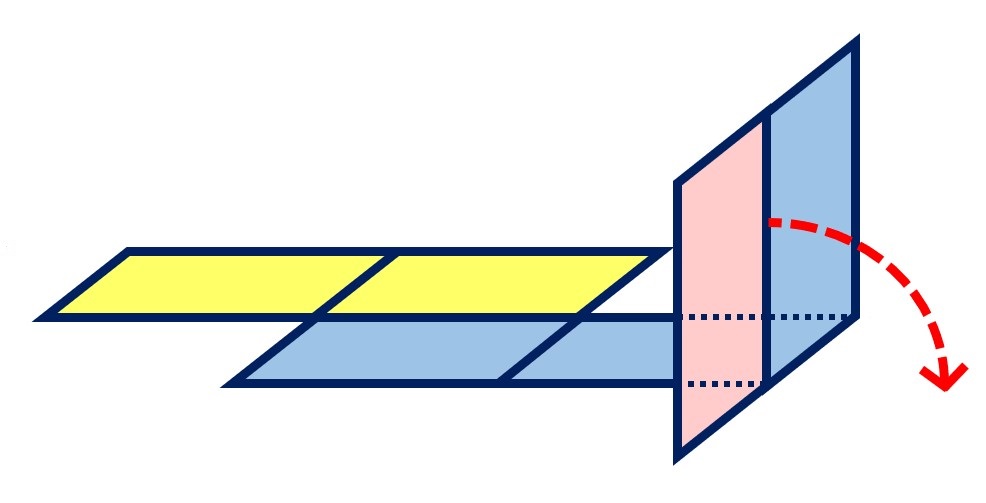
⑥紙の立方体の箱を、1枚の紙に広げることができました。
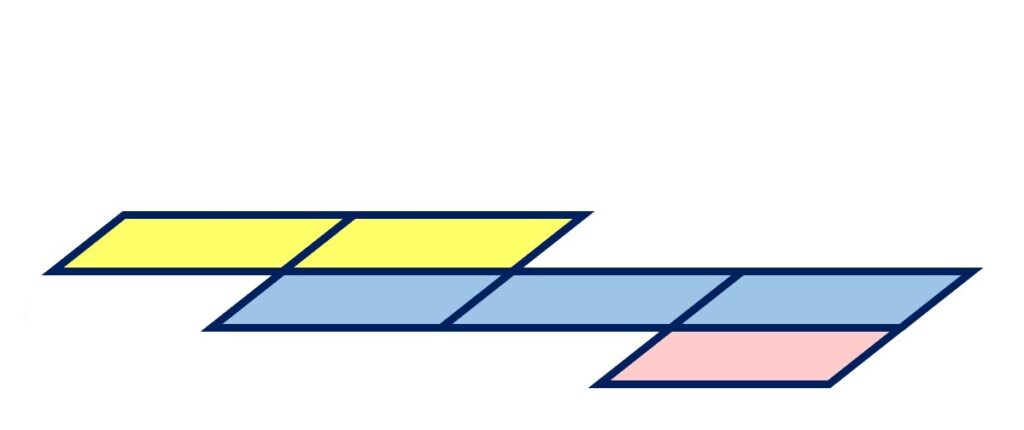
展開図(てんかいず)の基本
展開図とは、
と言いかえることもできます。
先ほどはななめから見ていた、展開した立方体。
真上からみてみると、
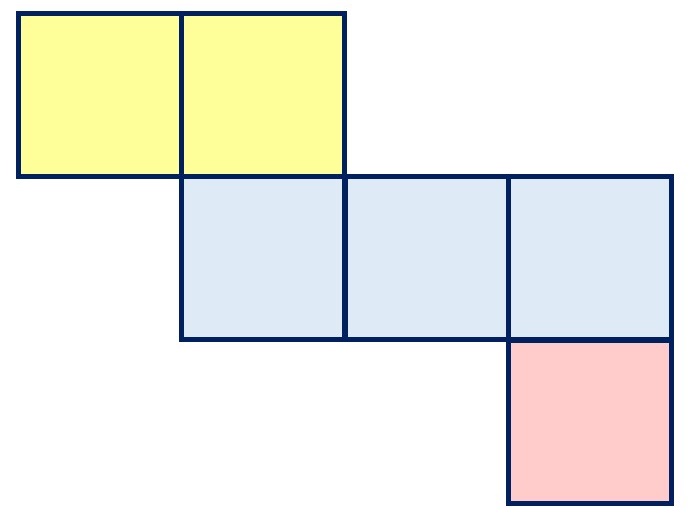
こうなります。


立方体を展開図にするときのポイントは、
●1枚の紙にする
ややこしくなりますし、
展開図とは呼べなくなってしまうのです。
立方体の展開図、パターンとルールで理解

説明したようにすれば
わかりやすくなるとはいえ、
立方体の箱をたくさん用意して、
切ってためして、
すべての展開図を作っていく
のは骨が折れます。
ですので、


やっぱり面倒じゃない……

4つのパターンとルールを
目で見てわかるよう
●位置が変わる(動く)正方形は3行目に。赤で色づけ
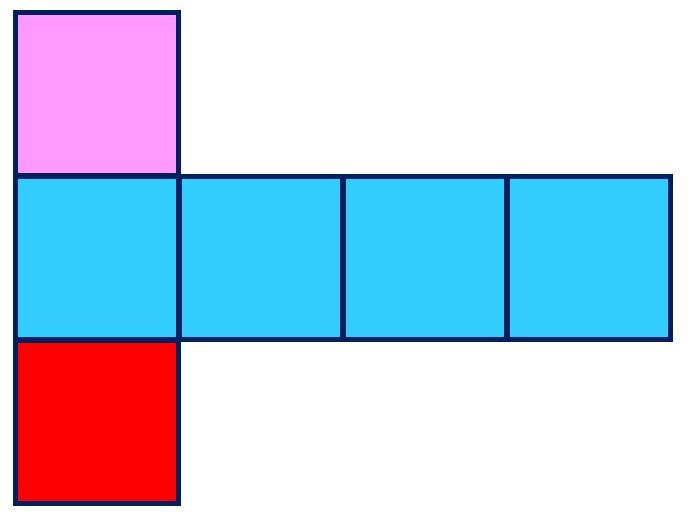
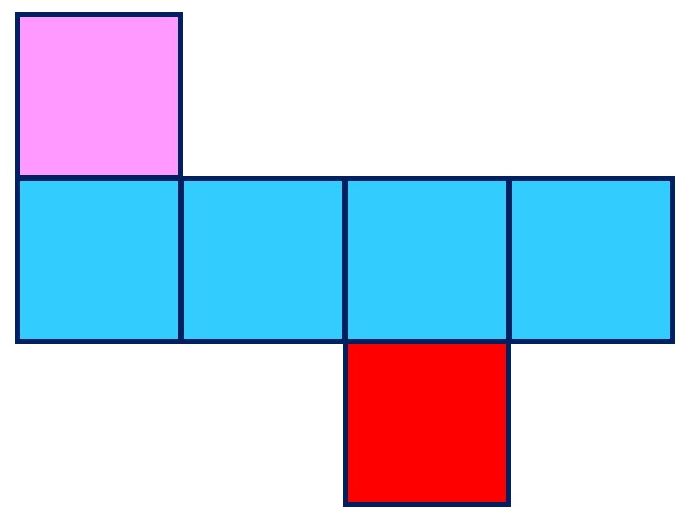
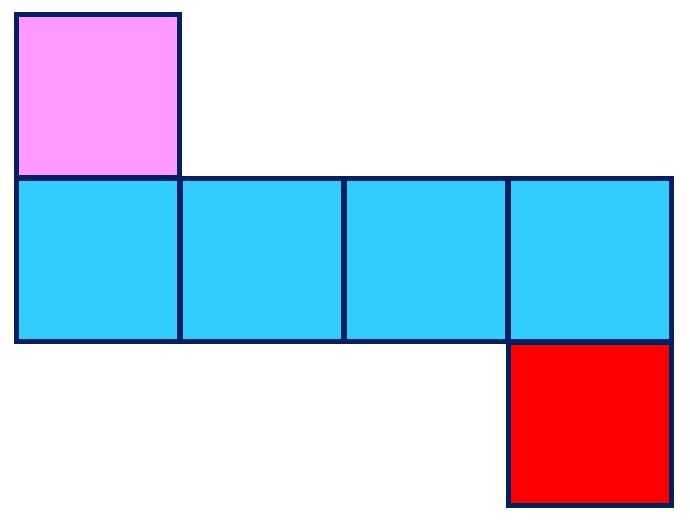
パターン1|中4個上はじ(4つ)
正方形が
二行目4つ、
三行目1つ
のパターン。
三行目は左から右に動かしています。
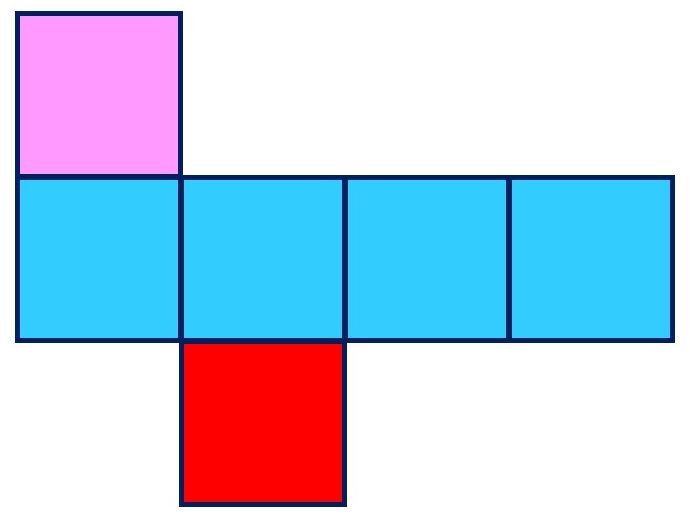
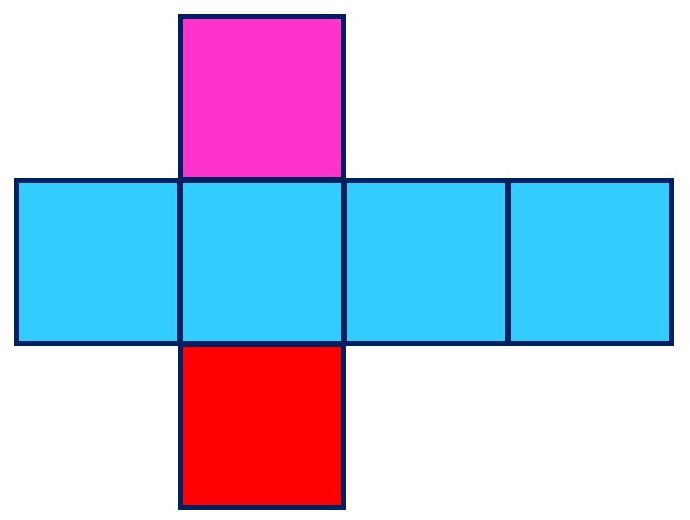
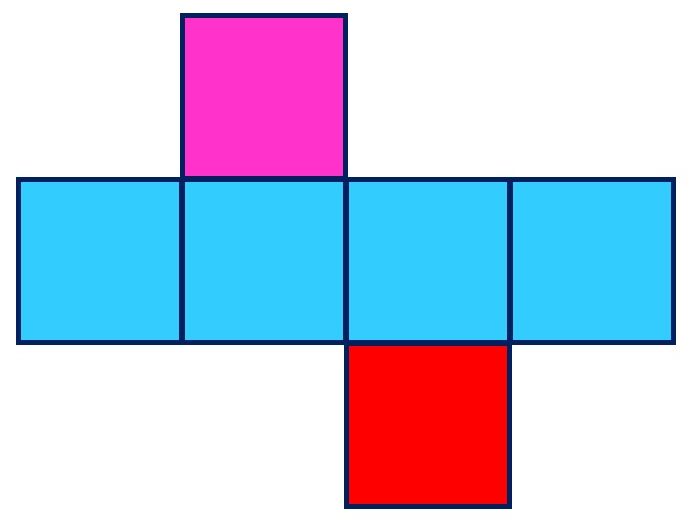
パターン2|中4個(2つ)
正方形が
二行目4つ、
三行目1つ
のパターン。
三行目は、まんなか2つだけです。
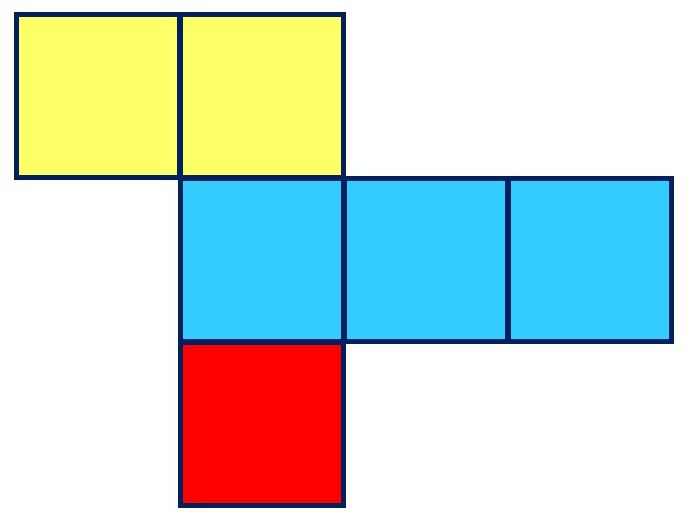
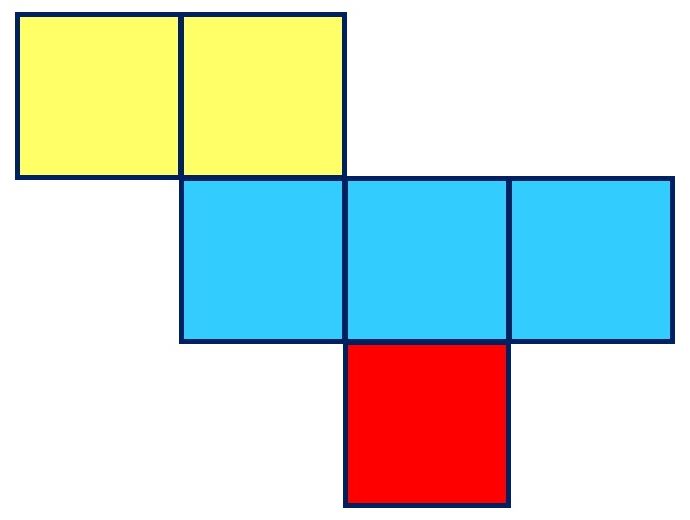
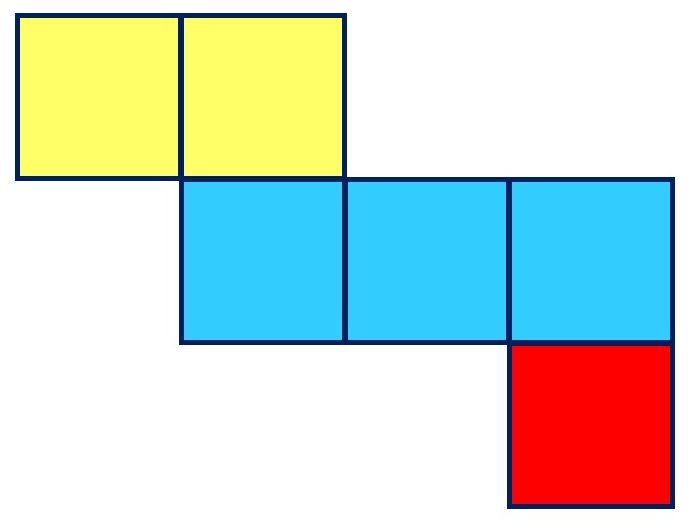
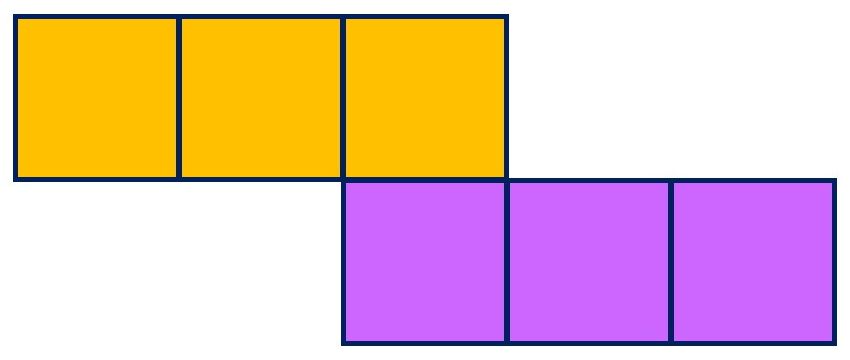
パターン3|中3個(3つ)
正方形が
二行目3つ、
三行目1つ
のパターン。
三行目は左から右に動かしています。
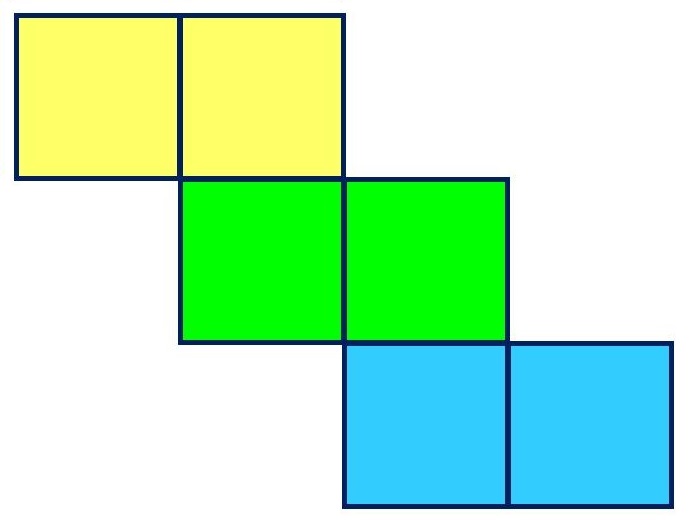
パターン4|その他(2つ)
パターン、
2つだけです。
もう迷わない!立方体の展開図“回転”“反転”

11種類の
のです。
とはいえ、もとの形は1つ。
回転と反転のルールさえ
分かってしまえば、
あとは簡単です。
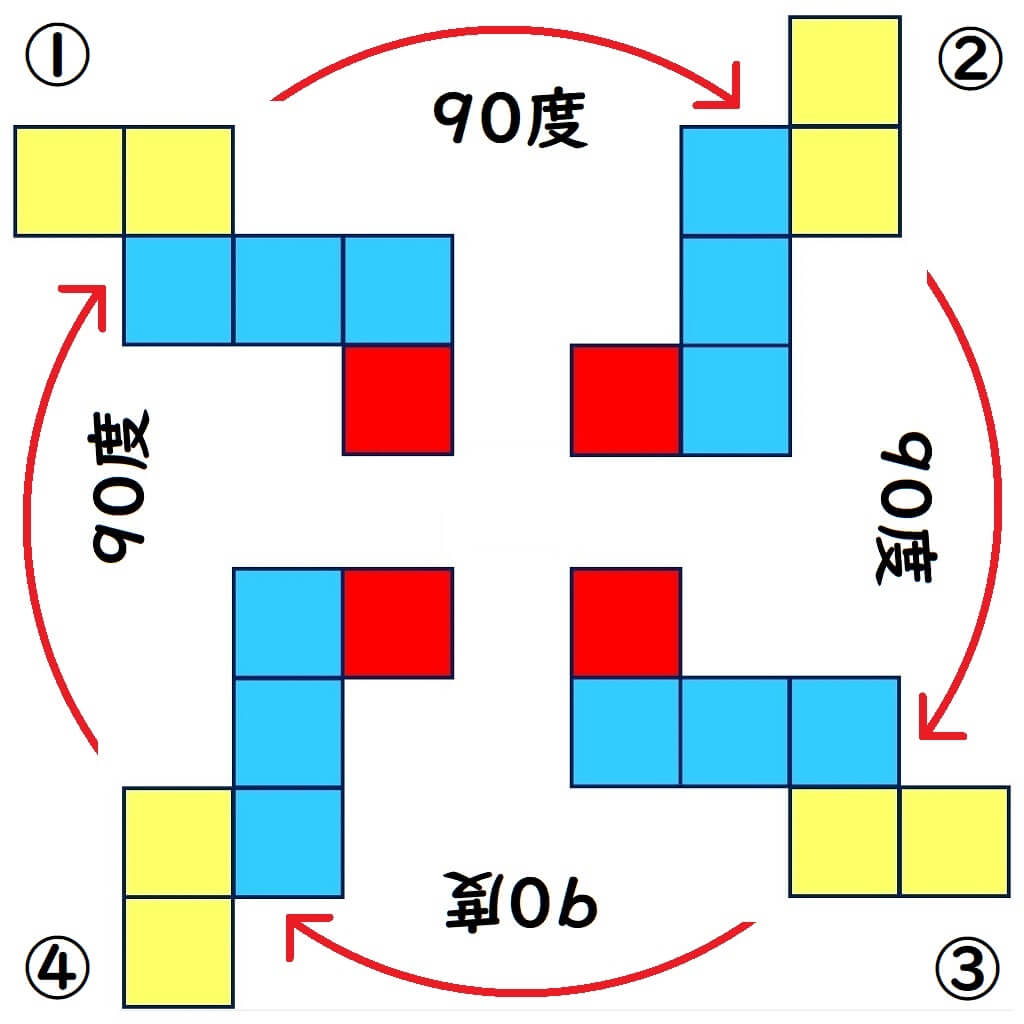
回転(かいてん)|90度
展開図パターン中3個の3番目を
90度回転させると、この4種類
になります。
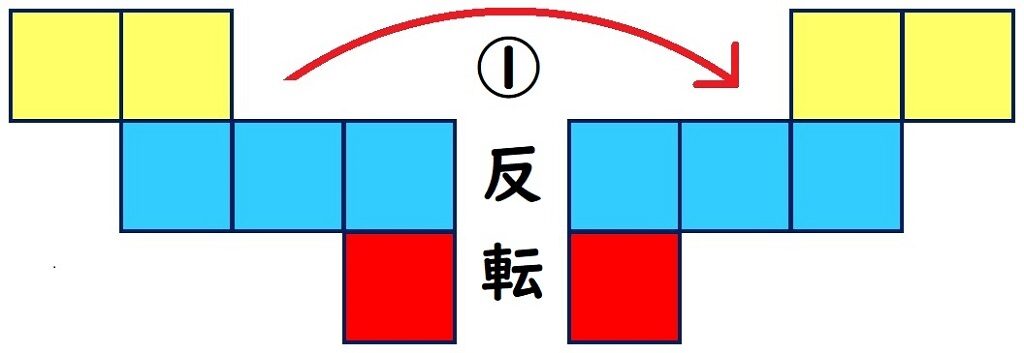
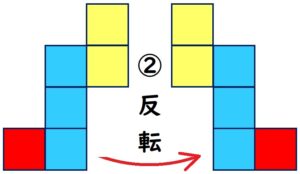
反転
回転させた4パターンを、それぞれ反転
するとこうなります。
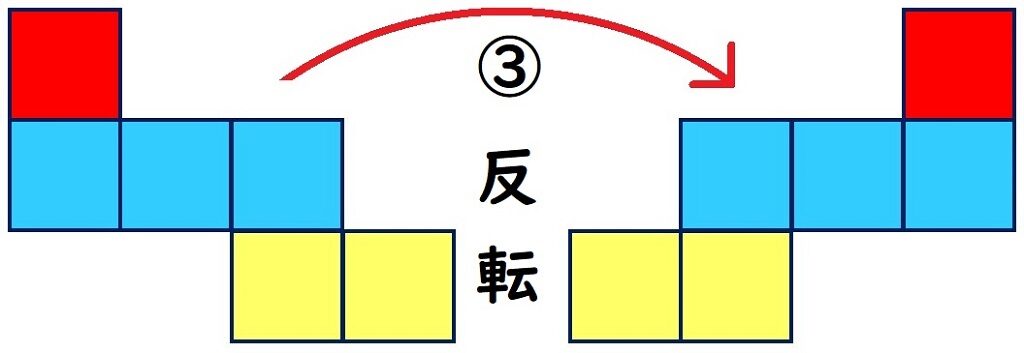
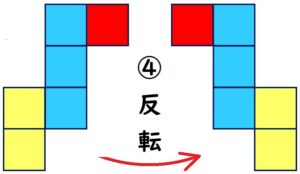

次は、例題を一緒に見ていきましょう!
これで完璧!“立方体の頂点”“展開図の点”の問題の解き方

“立方体の頂点”
“立方体展開図の点”の問題は、
良く出される問題の1つ。
ここでは、
例題で、基本の解き方を
わかりやすく解説
します。
例題1|一番遠い頂点(ちょうてん)
立方体の
ある頂点(かど)から
一番遠い頂点は
どこになるでしょうか?
例えば、下の見取図の
グリーンの頂点から
最も遠い頂点は、
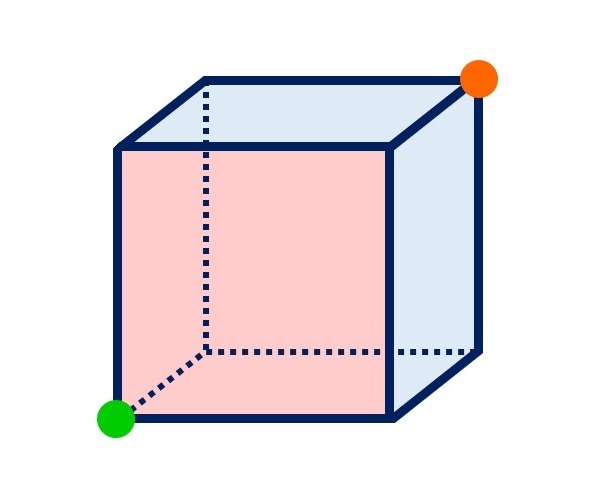
オレンジの頂点になります。
例題2|立方体の展開図、重なる点の問題の解き方
この立方体を
展開したとき、
グリーンの点と
オレンジの点は
どこにくる
でしょうか?
イメージが苦手な方も、
これから説明する
ルールをおさえれば
簡単に解ける
ようになります。
立方体だけでなく
すべての直方体
(六面体、直六面体、長方体)
で使えるルール。

見ていきましょう!
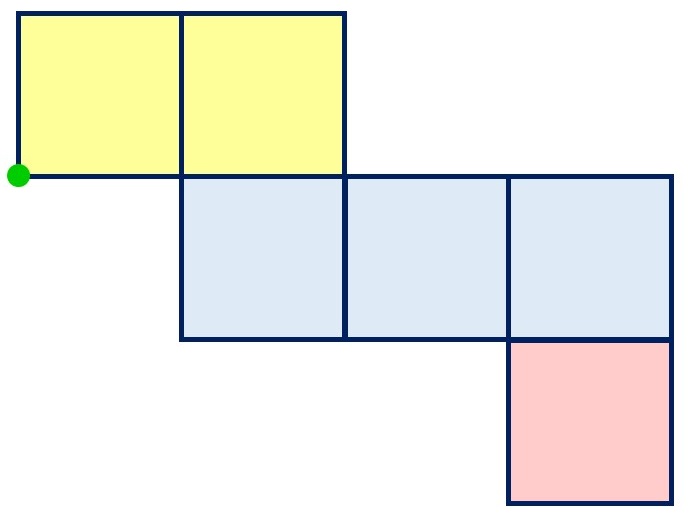
この状態で
グリーンの点から
一番遠い点を見つけるには
のです。
一番遠い点のパターンは
次の4つ!
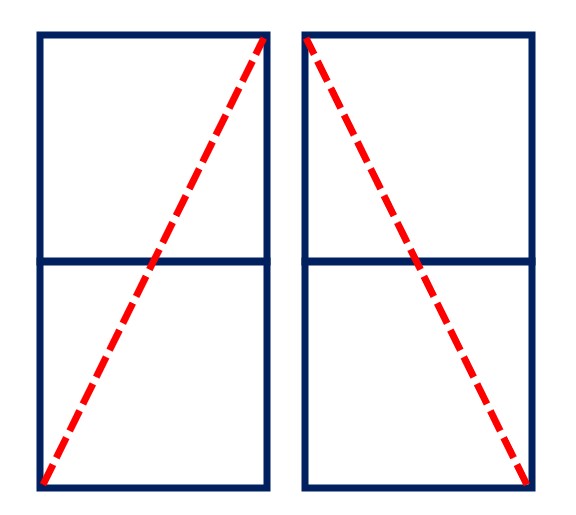
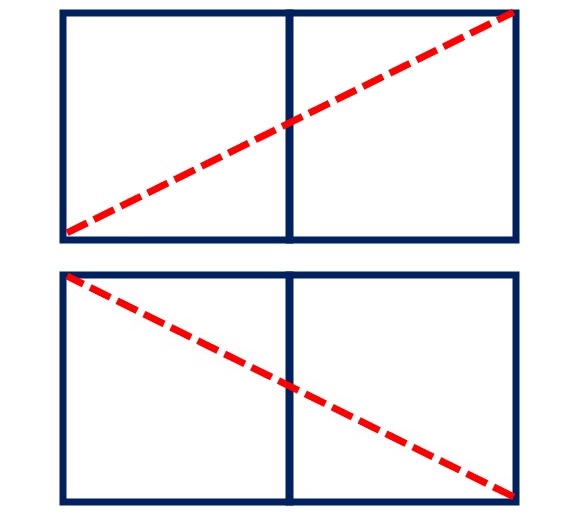
これを
のです。
さっそく
やってみましょう!
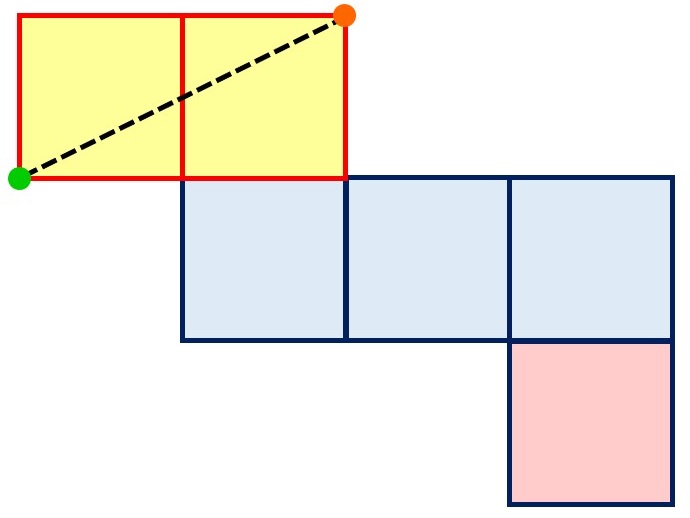
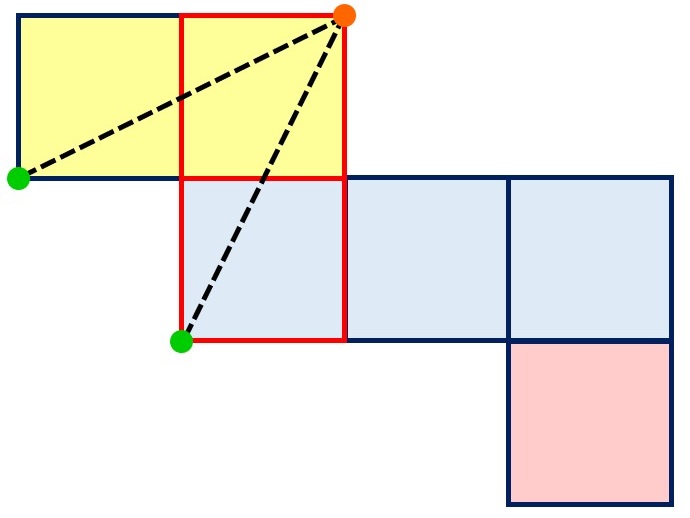
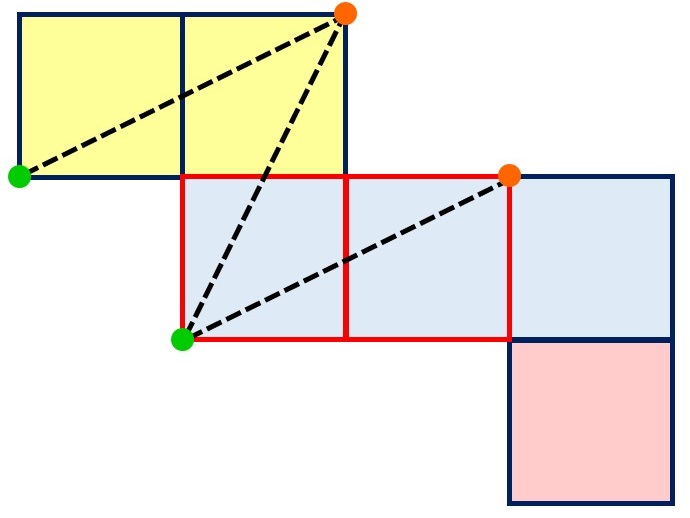
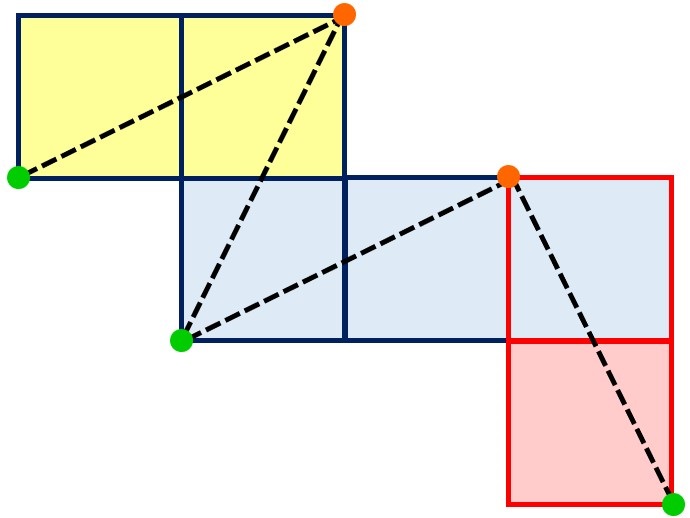
この展開図では
●オレンジの点2つが、グリーンから一番遠い頂点で1つに重なる
となります。
このルールは
のです!
ポイントは、
●引いた線は、2回通らないこと
●線は、途中で切らずにつなげていくこと
の3つです。


まとめ|立方体の展開図、4つのパターンで苦手解消

こちらの記事では
●立方体の展開図、苦手な人は4つのパターンで理解
●立方体の展開図、鏡にうつしても、回転しても、同じパターン
●これで完璧!“立方体の頂点”“展開図の点”の問題の解き方を例題で解説
それぞれの項目について、
新潟市中央区で
マンツーマン個別指導塾を
運営中の“のび校長”が
自作のオリジナルイラストを
使って解説してきました。
小学4年生の算数で
学びがスタートする立方体の問題は、
中学校、高校の数学の
基礎になるだけでなく、
入社試験や公務員採用試験などの
就職試験にも出題されます。
立方体と展開図を、
こちらの記事の内容にそって
理解していただければ
基本はバッチリ!
他の図形や立体の学習にも、
必ず役立つはずです。
記事の最後に
「豆知識|立方体の展開図、重なる2点の探し方」
もご紹介しています。
読んで頂いた皆さんの苦手意識が、
少しでも薄まれば幸いです。

ありがとうございました。
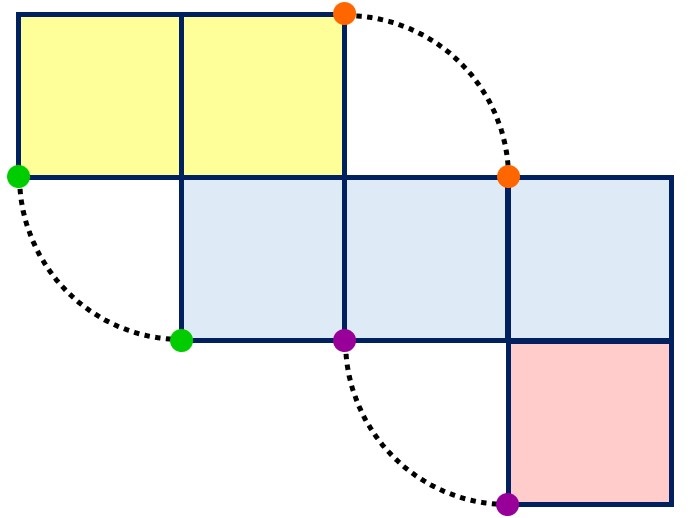
豆知識:立方体の展開図、重なる2点の見つけ方
立方体の展開図で、
重なる2つの点を探すには、
円の4分の1の弧(四分円の弧)を使う方法
が一般的。
ご存知の方も多いとは思いますが、
小学生向けに
念のためおさらい
しておきたいと思います。
例えば、下の3つの頂点。
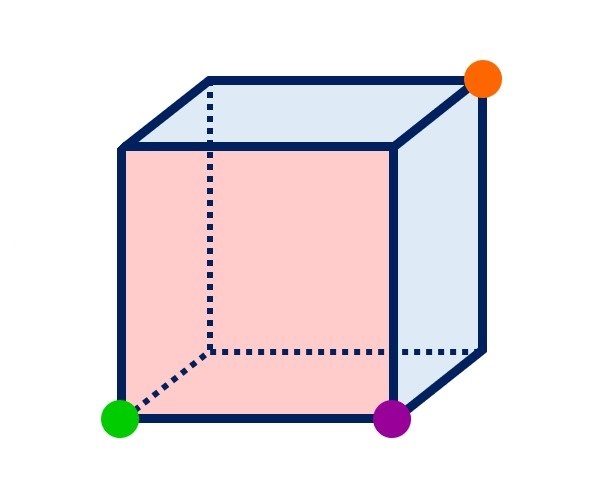
展開図には、3色の点が1つずつ描かれています。
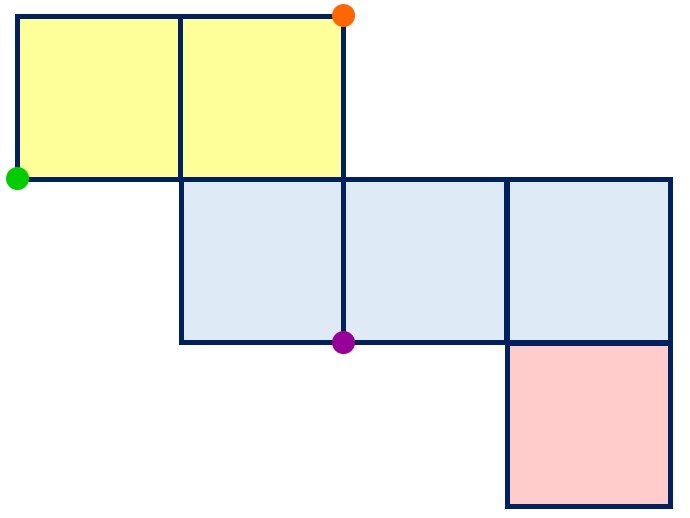
この3つの点
それぞれと重なる点を
探す時に、
四分円の弧を使うと
簡単に見つけられるのです。
いろいろな点を
自分で描いて
挑戦してみてくださいね!
中学数学の図形。解き方のポイントにつきましては、こちらの記事をご参照ください。
















