
連立方程式は、計算問題は余裕で解けるものの、文章問題は苦手という生徒さんが多い単元。
個別指導塾を新潟市で運営するスクールNOBINOBIの塾生さんからも

激ムズの問題ではありませんが、新潟県公立高校入試では、連立方程式の文章問題はほぼ毎年出題されています。
こちらの記事では、小学校の算数“つるかめ算”の中学生バージョン“連立方程式の文章問題の解き方”について、ポイントをしぼって説明。
苦手な、ごく普通の成績の生徒さん向けに、丁寧に解き方の基本を解説していきます。
記事の内容は
●文章問題の苦手克服に式をつくる練習が必要なわけ
●式をつくる手順と方法、主な例題3パターンで解説
●まとめ(注意点も)
この記事を書いたのは

●開校5年半で、新潟県内トップ私立高校合格者を輩出。
●年評定平均:中学時代3.7→高校進学後4.9、4.8の塾生を輩出。
●サポートした不登校の卒塾生、大学へ進学(卒業)。
●当ブログ、にほんブログ村カテゴリー「中学受験(個人塾)」
で、2020年6月から36ヶ月以上連続ランキング1位。
2020年3月開設15ヵ月目で月間4万PV超達成。
●元公立高校教員
●現役カウンセラー
こと“のびのび”。
よく出題される問題を例にして解説しますので、苦手を克服して数学得点アップにぜひ役立ててもらいたいと思います。
目次【タップでジャンプ】
連立方程式の文章題得点アップは、式をつくる練習が効果大!

連立方程式の問題で、

と感じる生徒さん、
新潟市のマンツーマン個別指導塾スクールNOBINOBI塾生さんの中にもたくさんいます。
そんな多くの“連立方程式の計算問題はできる”生徒さんたちは、
●式ができたら、計算はせずにまた別の問題で式をつくる。
●いろんなタイプの問題で、式をつくるまでの練習をくりかえす。
の3つを心がけてもらうと得点アップに効果大なのです。
連立方程式の文章題の苦手克服に式をつくる練習が必要なわけ

“計算はできる生徒さん”なら、文章題を読んで計算問題の形が作れれば、正答できるわけです。
令和2年度の新潟県公立高校入試では、1問3点の計算問題は10人中約9人が正答、一方、1問4点の文章問題は4人中約1人の正答でした。
これはあくまで一例ですが、文章題は計算問題をくりかえし練習しても解けるようにならないとも言えます。
ですから、文章問題を解けるようになりたいなら、計算練習と同じように“式をつくる”練習をしたほうが良いのです。
連立方程式の式のつくり方、具体的に解説

連立方程式の文章問題が苦手な人向けに、学校や塾などでは、「問題文をしっかり読む」「読解力をのばす」といったアドバイスをしてくれていると思います。


そんな皆さんのために、基本的な式のつくり方の手順をご紹介します。
連立方程式の基本的な式のつくり方の手順は
2.条件をすべて書きだす。
3.解りにくいならイラストや表を描いてみる。
4.求めるものをx(エックス)とy(ワイ)におきかえる。
5.イコール(=)の左側と右側が同じになる式を2つつくる。
の5つ。
連立方程式の文章題の出題パターンはたくさんありますが、ここでは代表的な
(2)割合
(3)道のり、速さ、時間
の3つのパターンについて、例題で実際に式をつくりながら手順を説明していきます。
(1)数と量の例題
次の例題を1~5の手順を使って式をつくってみます。
姉と弟は、それぞれ色鉛筆を持っている。この最初の状態から、姉が弟に3本の色鉛筆を渡すと、姉の色鉛筆の本数は弟の色鉛筆の本数の2倍になる。また、最初の状態から弟が姉に2本の色鉛筆を渡すと、姉の本数は弟の本数よりも25本多くなる。姉と弟が最初に持っていた色鉛筆の本数をそれぞれ求めなさい。
※平成31(令和元、2019)年度新潟県公立高校入試問題(改)
手順1.問題文を分ける。
まずはじめに“求めるもの”“式1”“式2”の3つを意識しながら、問題文を分けていきます。
この文は、
②この最初の状態から、姉が弟に3本の色鉛筆を渡すと、姉の色鉛筆の本数は弟の色鉛筆の本数の2倍になる。
③また、最初の状態から弟が姉に2本の色鉛筆を渡すと、姉の本数は弟の本数よりも25本多くなる。
④姉と弟が最初に持っていた色鉛筆の本数をそれぞれ求めなさい。
の4つに分けることができます。
①と④は、同じことを言っていますので、内容としては②、③、④の3つ(“式1”、“式2”、“求めるもの”)になります。
手順2.条件をすべて書きだす。
内容②、③、④の3つから条件を書きだすと、
②姉が弟に3本の色鉛筆を渡すと、姉の本数は弟の本数の2倍
③弟が姉に2本の色鉛筆を渡すと、姉の本数は弟の本数より25本多く
④姉と弟が最初に持っていた色鉛筆の本数
となります。
大事なところだけ書きだせばよいのです。
手順3.解りにくいならイラストや表を描いてみる。
解りにくいときは、イタズラ書き感覚でイラストを描いてみる。
例えば
②(式1)の条件は……
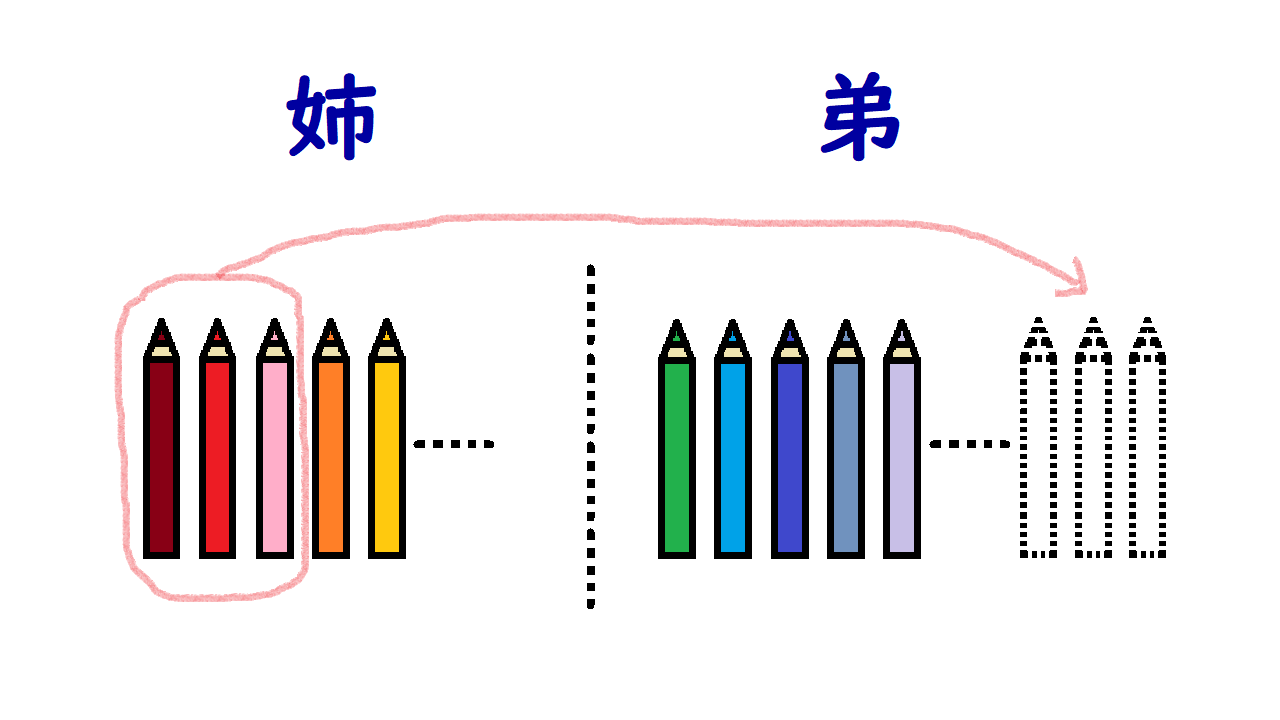
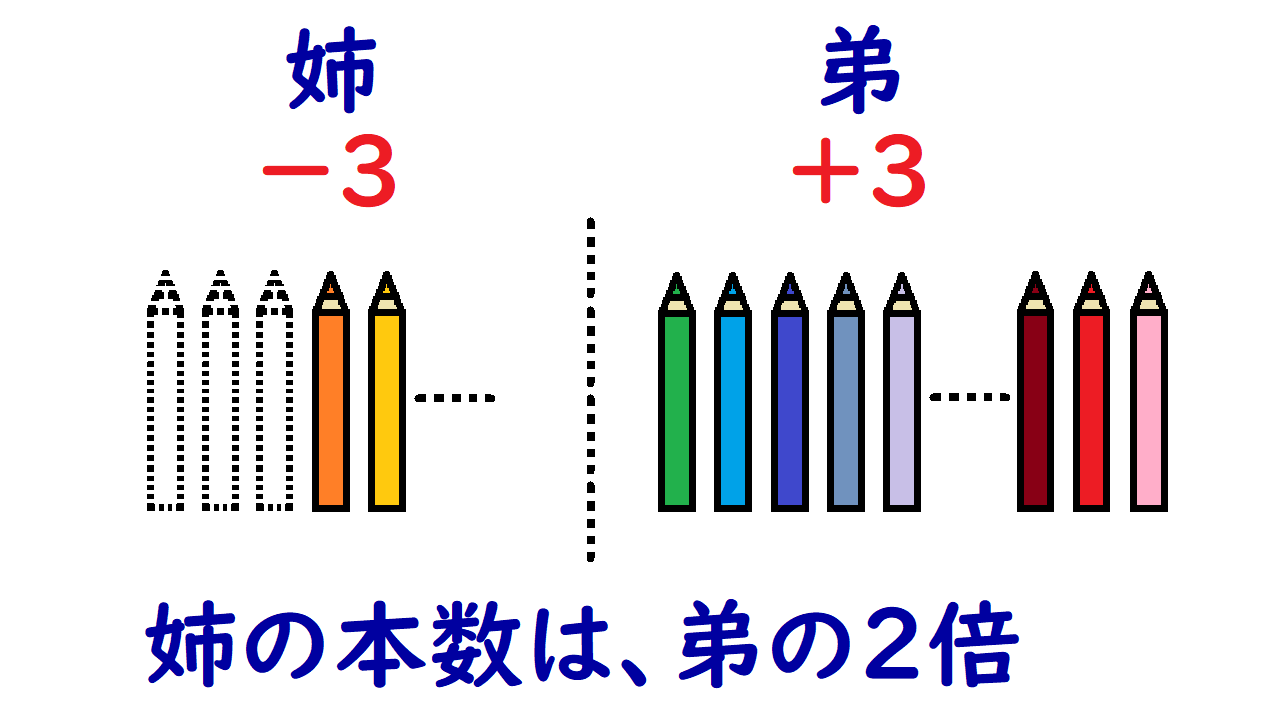
③(式2)の条件は……
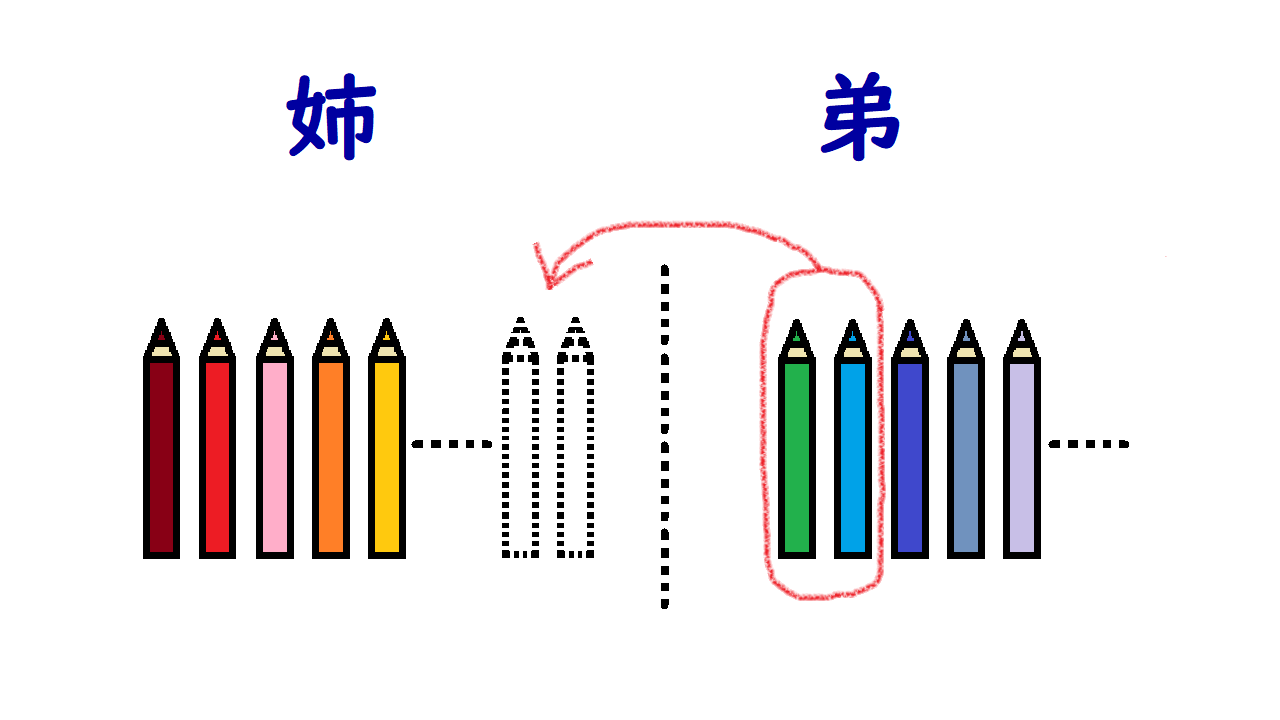
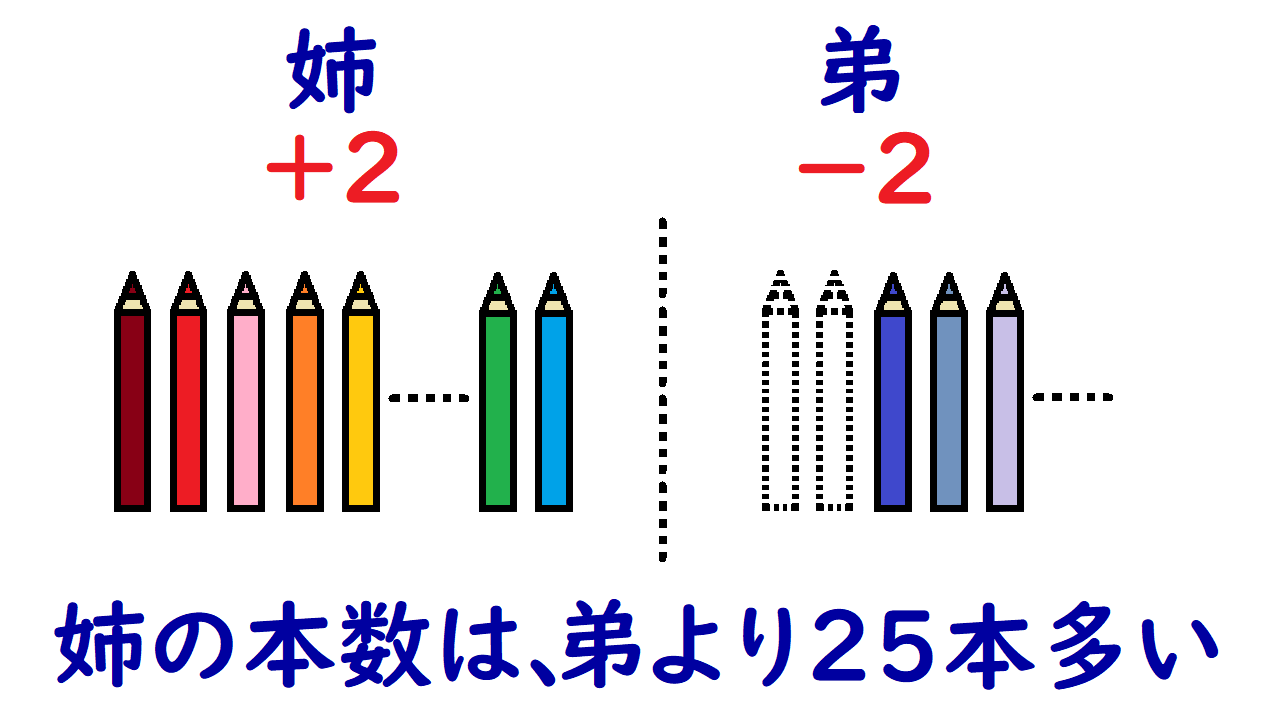
こんなイメージになります。
手順4.求めるものをx(エックス)とy(ワイ)におきかえる。
手順2の内容④の文“姉と弟が最初に持っていた鉛筆の本数”や手順3で描いたイラストから、
とします。
もちろん、逆にしても全く問題ありません。
求めるものを記号に置き換えられればいいのです。
手順5.イコール(=)の左側と右側が同じになる式を2つつくる。
手順2の内容②と③や、手順3のイラストから、式を2つつくります。
姉が弟に3本の色鉛筆を渡すと、姉の本数は弟の本数の2倍
ここから式1をつくります。
姉が弟に3本の色鉛筆を渡す=姉の本数は弟の本数の2倍
x-3=(y+3)+(y+3)
x-3=2(y+3)
整理すると
x-3=2y+6
移行して
x-2y=9
弟が姉に2本の色鉛筆を渡すと、姉の本数は弟の本数より25本多く
ここから式2をつくります。
弟が姉に2本の色鉛筆を渡す=姉の本数は弟の本数より25本多く
x+2=(y-2)+25
整理すると
x+2=y+23
移行して
x-y=21
これで
式1:x-2y=9
式2:x-y=21
の、2つの式をつくることができました。

(2)割合の例題
例題(1)と同じように、1~5の手順を使って式をつくってみます。
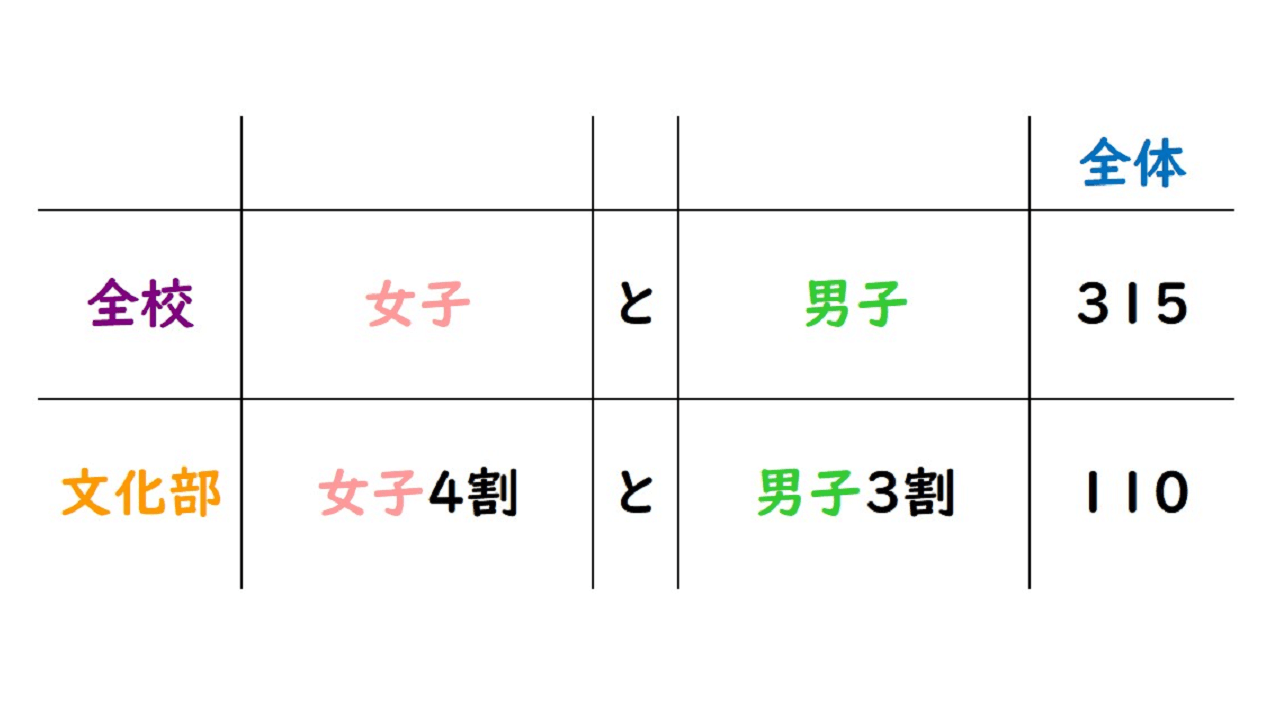
A校の生徒数は、女子男子合わせて315人です。そのうち女子の4割と男子の3割が文化部に所属していて、その人数は110人でした。A校の女子の生徒数と男子の生徒数をそれぞれ求めなさい。
手順1.問題文を分ける。
“求めるもの”“式1”“式2”の3つを意識しながら、問題文を分けます。
②そのうち女子の4割と男子の3割が文化部に所属していて、その人数は110人でした。
③A校の女子の生徒数と男子の生徒数をそれぞれ求めなさい。
の3つに分けられます。
①、②、③は、それぞれ“式1”、“式2”、“求めるもの”そのままになります。
手順2.条件をすべて書きだす。
内容①、②、③の3つの文から条件を書きだすと、
①生徒数は、女子男子合わせて315人
②女子の4割と男子の3割が文化部に所属、その人数は110人
③女子の生徒数と男子の生徒数
となります。
大事なところだけ書きだせばよいのです。
手順3.解りにくいならイラストや表を描いてみる。
解りにくいときは、表を描いてみると、グッと解りやすくなります。
まず、こんな感じで表の線をザックリ描きます。
そこに、手順2で書きだした条件①、②から、式の材料をすべて書き込み、表をうめていきます。
手順4.求めるものをx(エックス)とy(ワイ)におきかえる。
手順2の内容③の文“女子と男子の生徒数”から、
とします。もちろん逆にしても問題なし、求めるものを記号に置き換えられればいいのです。
手順5.イコール(=)の左側と右側が同じになる式を2つつくる。
手順2の内容②と③や、手順3の表から、式を2つつくります。
天順3の表の単語に、手順4で決めたxとyを当てはめると……
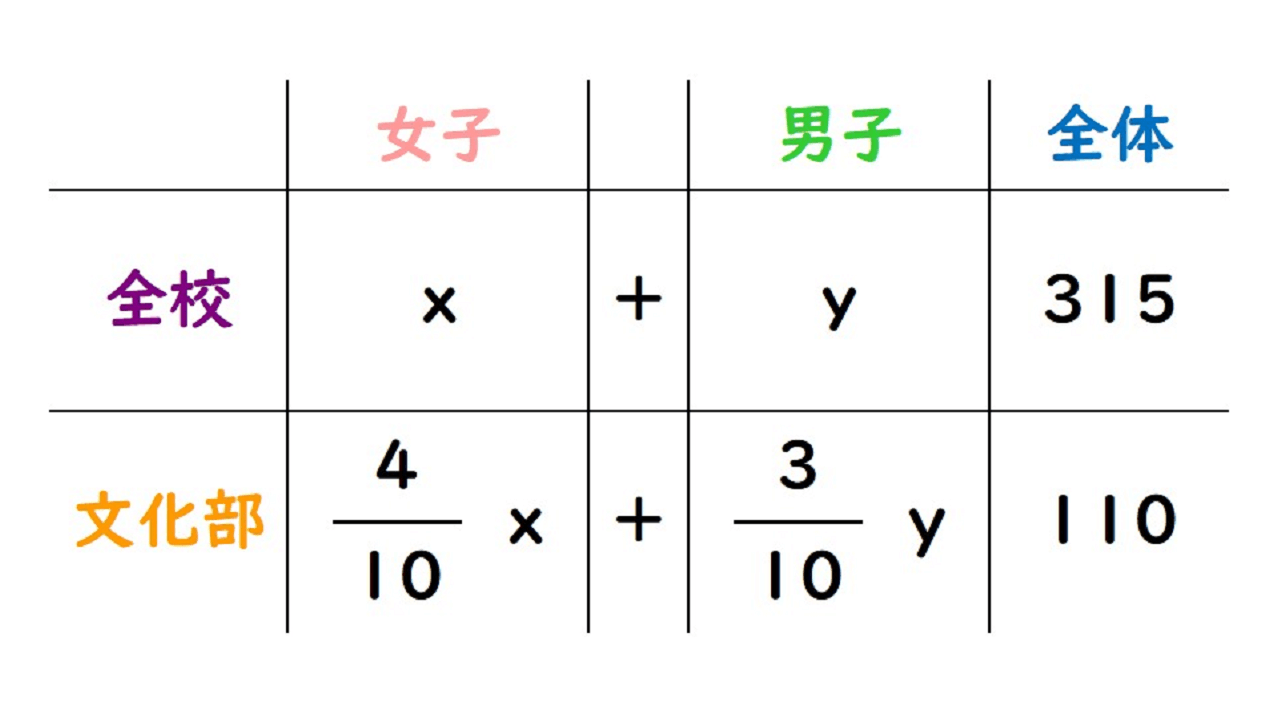
こうなると思います。あとは、式をつくっていくだけです。
生徒数は、女子男子合わせて315人
ここから式1をつくります。
x+y=315
女子の4割と男子の3割が文化部に所属、その人数は110人
ここから式2をつくります。
※“ / ”は、分数のよこ棒記号のかわりです。
4/10x+3/10y=110
分数を整数にしたいので、=の両側に10をかけ算して
4x+3y=1100
これで
式1:x+y=315
式2:4x+3y=1100
の、2つの式をつくることができました。

(3)道のり、速さ、時間の例題
例題(1)・(2)と同じように1~5の手順を使って式をつくってみます。
B校の社会科で乳製品工場、日本酒の蔵元の順でバスで見学することになりました。学校から蔵元までの道のりは80㎞です。バスは午前8時に学校を出発し、工場まで時速40㎞で走りました。工場を1時間見学した後、時速50㎞で走ったところ、蔵元に10時45分に到着しました。B校から工場、工場から蔵元までの道のりをそれぞれ求めなさい。
手順1.問題文を分ける。
“求めるもの”“式1”“式2”の3つを意識しながら、問題文を分けます。
①学校から蔵元までの道のりは80㎞です。
②バスは午前8時に学校を出発し、工場まで時速40㎞で走りました。
③工場を1時間見学した後、
④時速50㎞で走ったところ、蔵元に10時45分に到着しました。
⑤B校から工場、工場から蔵元までの道のりをそれぞれ求めなさい。
はじめの説明文をのぞくと、5つの文に分けられます。
①~⑤を使って、“式1”、“式2”、“求めるもの”の条件を書きだしていきます。
手順2.条件をすべて書きだす。
内容①~⑤の5つの文から条件を書きだすと、
①学校から蔵元までの“ 道のりは80㎞ ”
② “ 午前8時 ” に学校を出発、工場まで “ 時速40㎞ ” で走り
③工場を “ 1時間 ” 見学
④ “ 時速50㎞ ” で走り、蔵元に “ 10時45分 ” に到着
⑤B校から工場、工場から蔵元までの “ 道のり ”
となります。
例題(1)、(2)より複雑に見えますが、同じように大事なところだけ書きだします。
このパターンの問題では、タイトルどおり“道のり”、“速さ”、“時間”の3つの条件が出てきます。
式1、式2、求めるものの3つを意識しながら
どの材料がどの条件か、自分でわかるように印をつけておく
と、解きやすくなります。
手順3.解りにくいならイラストや表を描いてみる。
解りにくいときは、イラストや表を描いてみると、グッと解りやすくなります。
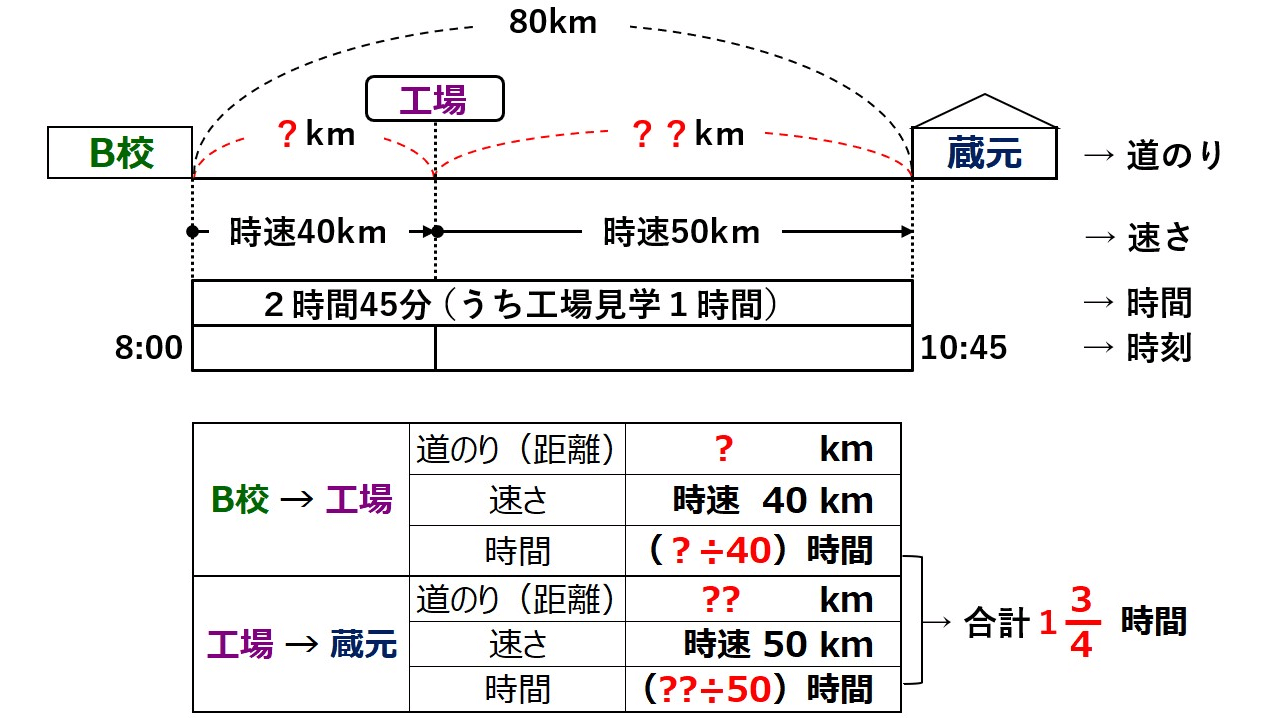
自分でわかりやすければ、この通りでなくても大丈夫。
丁寧に描く必要もないのです。
手順4.求めるものをx(エックス)とy(ワイ)におきかえる。
手順2の内容⑤の文や図表から、
工場から蔵元までの道のりをy
とします。もちろん逆にしても問題なし、求めるものを記号に置き換えられればいいのです。
手順5.イコール(=)の左側と右側が同じになる式を2つつくる。
手順2の内容②と③や、手順3の図表から、式を2つつくります。
学校から蔵元までの“ 道のりは80㎞ ”
学校から蔵元までの道のりと時間はわかっていますので、ここから式1をつくります。
x+y=80
時間に注目
時刻と時間に注目して式2をつくります。
※“ / ”は、分数のよこ棒記号のかわりです。
手順2の内容②と③や、手順3の図表から、
学校を8時に出発して10時45分に蔵元に到着しているので、総時間は2時間45分なのがわかります。
ただ、そのうち工場で1時間見学したので、その間は移動なし。
総時間2時間45分-見学時間1時間=1時間45分
これが移動にかかった時間です。
速さの単位は、1時間あたりの距離“時速”ですので、分を使わず“時間”であらわさないと計算できません。
なので、1時間45分を1+3/4時間とします。
学校から工場までの移動時間と工場から蔵元までの移動時間をたすと、1+3/4時間になるわけです。
道のりを速さでわれば、時間が計算できます。
x/40+y/50=1+3/4(4分の3)
x/40+y/50=7/4
分数を整数にしたいので、=の両側に200をかけようと思います。
200×(x/40+y/50)=200×(7/4)
5x+4y=350
これで
式1:x+y=80
式2:5x+4y=350
の、2つの式をつくることができました。

まとめ

こちらの記事では“連立方程式の文章問題の解き方”について、ポイントをしぼって丁寧に解き方の基本を解説しました。
記事の内容は、計算はできるけど文章題が苦手なごく普通の生徒さん向けに
●文章問題の苦手克服に式をつくる練習が必要なわけ
●式をつくる手順と方法、主な例題3パターンで解説
2.条件をすべて書きだす。
3.解りにくいならイラストや表を描いてみる。
4.求めるものをx(エックス)とy(ワイ)におきかえる。
5.イコール(=)の左側と右側が同じになる式を2つつくる。
の5つでした。
実は、中学生の数学、1年生範囲の“一次方程式の利用”の、こちらの記事で取りあげた手順とほとんどかわらないのです。
変わるのは、連立ですので手順5の“式を2つつくる”というところだけ。
この記事で取りあげた連立方程式の文章題例題は基本の3つ、出題パターンは他にもたくさんあります。
ですが、この基本の手順さえおさえておけば、どんな問題でも式をつくれるようになります。
連立方程式の文章問題は、
これができれば、8割は解けたようなもの。
注意点は、
●単位をしっかり確認、間違えないようにそろえる。
●求めるものxとyは何なのか、必ず書く。
●等しい関係をさがしだす。
●計算ミスに気をつける。
- 数や量を文字(x、y)に変えられない、
- 何度読んでも、何を言っているのか読み取れない、
- 単位をそろえられない、
- 割合、速さ、平均、面積などの求め方がわからない、
という生徒さん達は、残念ながらこちらの記事を読んでも解けるようにはなりません。
まず国語や算数レベルの復習から取りかかる必要があると考えます。
計算はできるけど文章題が苦手、そんなごく普通の生徒さんたちの

最後までお読みいただきありがとうございました。













