
中学数学の基本「一次方程式」。
方程式の「利用」や「応用」というかたちで、文章問題が出題される単元でもあります。
別の記事でご紹介した通り、文章問題は主に8種類。
初めて訪問してくれた皆さんのために「良く出題される順」をご紹介すると、
②代金・個数に関する問題
③過不足に関する問題
④年齢・分配・貯金に関する問題
⑤自然数・整数に関する問題
⑥割合に関する問題
⑦図形に関する問題
⑧平均に関する問題
となります。
新潟市で運営中の個別指導塾の塾生さんたちには、とくに良く出題される
①道のり・速さ・時間に関する問題
の解説に力を入れていますが、出題パターンが多く

な生徒さんたちもいます。
そこでこちらの記事では単元「一次方程式の利用」の「道のり・速さ・時間」の基本の問題を取りあげます。
- 記事の内容は、
●「道のり・速さ・時間」の主な出題タイプは
「おいつく」「まわる」「かわる」の3つ。
●「まわる」のうち「であう」問題の解き方、解き方の手順にそって解説。
●「まわる」のうち「おいつく」問題の解き方、解き方の手順にそって解説。
●まとめ
となっています。
この記事を書いているのは、

●開校5年半で、新潟県内トップ私立高校合格者を輩出。
●年評定平均:中学時代3.7→高校進学後4.9、4.8の塾生を輩出。
●サポートした不登校卒塾生、定時制高校→大学進学。
●当ブログ、にほんブログ村カテゴリー「中学受験(個人塾)」
で、2020年6月から5ヶ月連続ランキング1位を獲得。
●元公立高校教員
●現役カウンセラー

[outline]
「道のり・速さ・時間」の主な出題タイプ3つ

「道のり・速さ・時間」の問題には多くの種類があります。
その中でも代表的な問題は
先に出発した人に後から追いかける人が「おいつく」タイプ、
二人がグランドや池などの周囲を「まわる」タイプ、
途中で速さや手段が変化する「かわる」タイプの3タイプ。
ここでは「まわる」タイプの例題2種類について、解きながら解説していきます。
苦手な人向けに基本的な考え方を理解してもらうための内容ですので、

という箇所は、どんどん飛ばして読み進めてください。


「まわる」問題のうち「であう」の解き方

まずは「まわる」タイプの問題2種類のうち「であう」例題を、解き方の手順にそって解きながら解説していきます。
「であう」の例題
1周2kmのため池。
同じ地点に立っていたソラさんとレイナさん。
反対方向へ同時に出発しました。
ソラさんは右まわり(時計回り)、自転車で毎分200m、
レイナさんは左まわり、徒歩で毎分50m進みます。
2人が出発してから初めて出会うのは何分後でしょうか。
一次方程式文章問題の解き方は、
② 条件をすべて書きだす。
③ 解りにくいときは、絵や図を描いてみる。
④ 求めるものをx(エックス)におきかえる。
⑤ 「=(イコール)」の左側と右側が同じになるように式をつくる。
ソラさんとレイナさんは反対方向へ同時に出発
ソラさん:右まわり(時計回り)、自転車で毎分200m
レイナさん:左まわり、徒歩で毎分50m
2人が初めて出会うのは何分後?
となります。
ニガテな人はこれだけでは解きにくいと思います。
③解りにくいときは、絵や図を描いてみるとグッとわかりやすくなります。
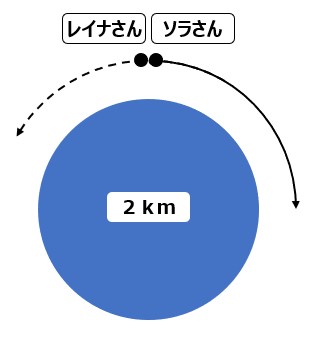
④求めるものをxとすると…
上のように円で描けばイメージをつかむには良いのですが…
ここに条件を色々書き込んでいくと、ゴチャゴチャしてわかりにくくなってしまいます。
そこで、スタート地点でちょん切って、直線にしてみました。
出発点は、同じ場所です。
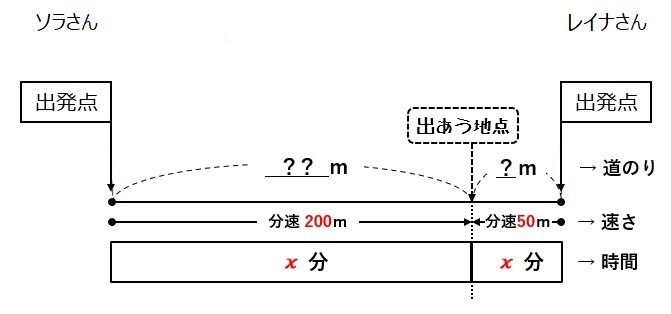
図に書き込んでもわかりにくい場合は、ソラさん、レイナさんそれぞれの道のり(距離)、速さ、時間を表にしてみるのも良い方法です。
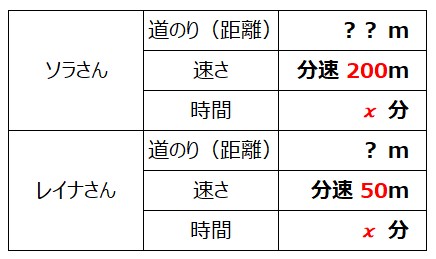

あと一つ、式をつくるための材料が残っています。
そう、このため池は1周2kmでした。
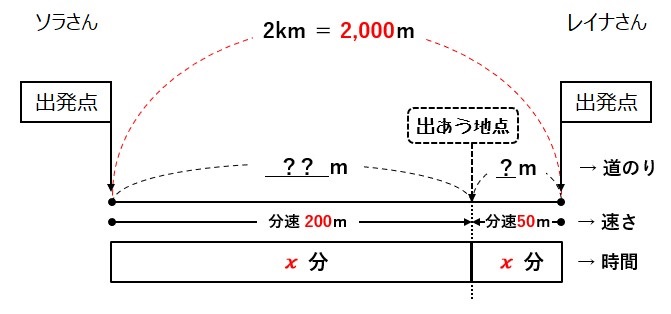
ソラさんが進んだ道のりとレイナさんが進んだ道のりを合わせるとちょうど1周になります。
あとは⑤「=(イコール)」の左側と右側が同じになるように式をつくることができれば x がだせるはず。
ソラさんの道のりとレイナさんの道のりを合わせれば、ため池一周の道のりになりますから、

この式を解けば、2人がかかった時間 x をもとめることができます。
250x = 2000
「=」の両側を250でわれば、xがもとめられます。
250x ÷ 250 = 2000 ÷ 250
x = 4
ことがわかりました。
「まわる」問題のうち「おいつく」の解き方

池やグランドを「まわる」問題では「であう」のほかに、速さがちがう2人が同じ方向に進んで「おいつく」タイプの問題も良く出題されます。
「まわる」タイプの問題のうち「おいつく」例題を、解き方の手順にそって解きながら解説していきます。
「おいつく」タイプの問題は別の記事でも取りあげましたが、周囲を「まわる」タイプはこちらで取りあげています。
まわって「おいつく」例題
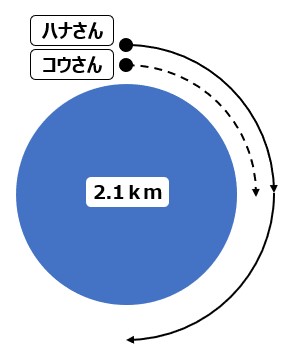
1周2.1kmのため池。
同じ地点にいたハナさんとコウさん。
同じ方向へ同時に出発しました。
ハナさんは、自転車で毎分200m、
コウさんは、徒歩で毎分50m進みます。
ハナさんがコウさんに追いつくのは何分後でしょうか。
この問題も一次方程式文章問題の解き方5つの手順で解いていきます。
ソラさんとレイナさんは同じ方向へ同時に出発
ハナさん:自転車で毎分200m
コウさん:徒歩で毎分50m
ハナさんがコウさんに追いつくのは何分後?
となります。
ニガテな人はこれだけでは解きにくいと思います。
③解りにくいときは、絵や図を描くとグッとわかりやすくなります。
「同じ方向に進んで追いつく」ということは
速い人が遅い人より1周多く進むから追いつく
わけです。
このタイプの問題は、池のまわりの道のりと2人の速さが変わっても道のりの差はちょうど1周。
ですから、
同じ方向に進んで追いつく場合:2人の道のりの差=1周分
ということになります。
④求めるものをxとすると…
分かりにくいときは、問題文を読んでわかることを図に書き込んでいきます。
ただ、円で描いてしまうと道のりをグルグル書くことになり、わかりにくくなりがち…
そこでこの例題でも、道のりを切ってのばして直線にしてみると、
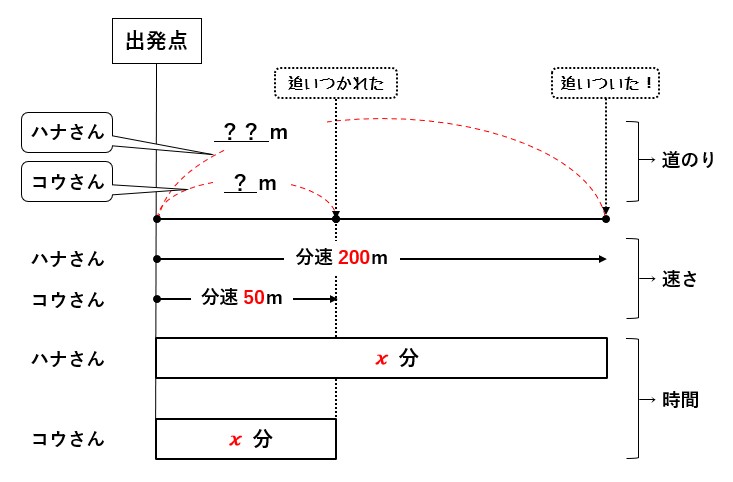
こんなふうに描くことができます。
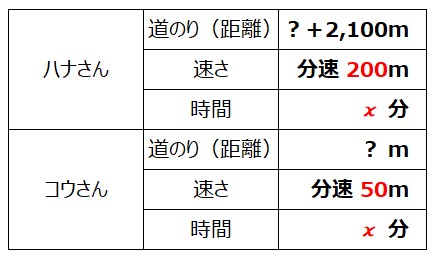
図に書き込んでもわかりにくい場合は、ハナさん、コウさんそれぞれの道のり(距離)、速さ、時間を表にしてみましょう。
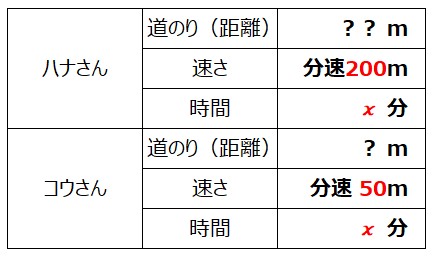

あと一つ、式をつくるための材料がありました。
そう、このため池は1周2.1km。
2人の道のりの差=1周分でしたので、
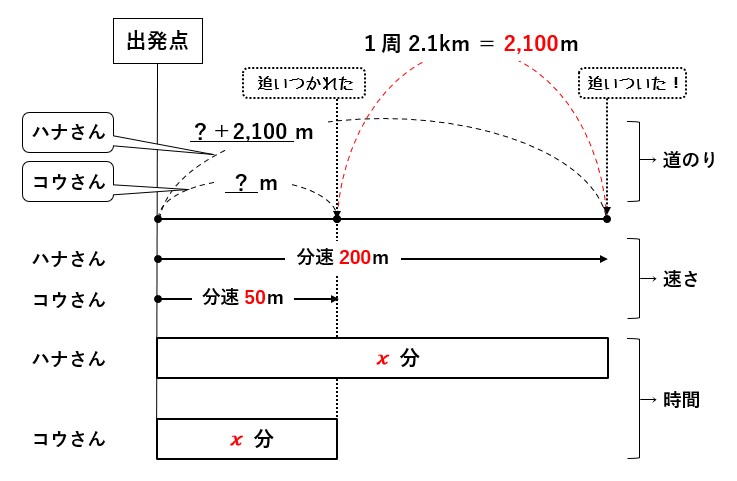
ですので⑤「=(イコール)」の左側と右側が同じになるように式をつくることができれば x がだせるはず。
ハナさんの道のりからコウさんの道のりを引けば、ため池一周の道のりになりますから、
200x - 50x = 2100

あとは、この式を解けば、2人がかかった時間 x をもとめることができます。
150x = 2100
「=」の両側を150でわればxがもとめられます。
150x ÷ 150 = 2100 ÷ 150
x = 14
ことがわかりました。

まとめ

こちらの記事では単元「一次方程式の利用」の「道のり・速さ・時間」の基本の問題を取りあげて解説してきました。
記事の内容は、
●「道のり・速さ・時間」の主な出題タイプは
「おいつく」「まわる」「かわる」の3つ。
●「まわる」のうち「であう」問題の解き方、解き方の手順にそって解説。
●「まわる」のうち「おいつく」問題の解き方、解き方の手順にそって解説。
●まとめ
一次方程式文章問題の解き方
② 条件をすべて書きだす。
③ 解りにくいときは、絵や図を描いてみる。
④ 求めるものをx(エックス)におきかえる。
⑤ 「=(イコール)」の左側と右側が同じになるように式をつくる。

ここで取り上げた問題の解き方を参考に、数学の実力アップにつなげて頂ければ幸いです。
「道のり・速さ・時間」の主な出題タイプ「おいつく」問題の解き方は、以下の記事をご参照ください。
「一次方程式の利用」濃度の文章問題の解き方は、以下の記事をご参照ください。
[sitecard subtitle=関連記事 url=https://school-nobinobi.com/calculate-the-concentration-using-a-linear-equation/ target=self]理科ででてくる「濃度」の基本を説明している以下の記事もご参照ください。
[sitecard subtitle=関連記事 url=https://school-nobinobi.com/application-problems-of-linear-equations-for-concentration/ target=self]

皆さんのお役に立てれば幸いです。














