
中学の数学。
図形の学習では
「三角形と四角形」
を勉強します。
新潟市の個別指導塾
スクールNOBINOBIの
塾生さんたちの中には、
数学が苦手な生徒さんだけでなく、
苦手ではないのに
のんさん

な生徒さんもいます。
そこで、こちらの記事では
中学数学の
します。
例題として取り上げるのは、
“平行線と面積”
の問題のうち、
面積はそのままで形を変える
“等積変形”
の問題。
教科書や参考書でも
取り上げられていて、
テストでも
比較的良く出されます。
記事の内容は
「問題文を小分けにする」「図を描く」「図に条件を書き込む」の3つ。
●面積はそのままで形を変える“等積変形”問題の解き方
解き方のポイントにそって、手順図で詳しく解説。
●まとめ

チャレンジしてみようかな……
記事を書いているのは、

●小中学生対象完全個別指導塾の校長(経営者兼専任講師)
●開校5年半で、新潟県内トップ私立高校合格者を輩出。
●年評定平均:中学時代3点台→高校進学後4.9、4.8、4.4の塾生を輩出。
●サポートした不登校の卒塾生、4年制大学へ進学(卒業)。
●オリジナル直筆記事が、グーグル3ワード検索で1位(2024.5.1現在)
●当ブログ、にほんブログ村カテゴリー「中学受験(個人塾)」
で、2020年6月から36ヶ月以上連続ランキング1位。
2020年3月開設15ヵ月目で月間4万PV超。
●元公立高校教員
●現役カウンセラー
こと“のびのび”。

という人は、
どんどん読み飛ばしてください。
目次【タップでジャンプ】
中学数学の図形問題の解き方、ポイントは?

図形問題の解き方ポイント
を一言でまとめると、
視覚化です。
なぜ視覚化で解きやすくなるのか?
問題文で読んだことを
実際に手を動かして図を描き、
その図に条件を書きこめば、
普段人間が日々一番使っている
五感の一つ
“視覚”に訴える
ことができます。
その結果
ミスを減らすことができるのです。
スクールNOBINOBIでも
頭の中だけで
考えて答えようとする
塾生さんたちほど
ケアレスミス
したり、
勘違いで間違えたり、
解けなかったりするケースが
とても多くて

と感じています。
の記事の繰り返しになりますが
正答率アップには
② 図を描く。
③ 図に条件を書き込む。

中学数学の図形問題|面積そのまま形を変形“等積変形”例題

ここでは例題を、
解き方の手順にそって
解きながら解説
していきます。
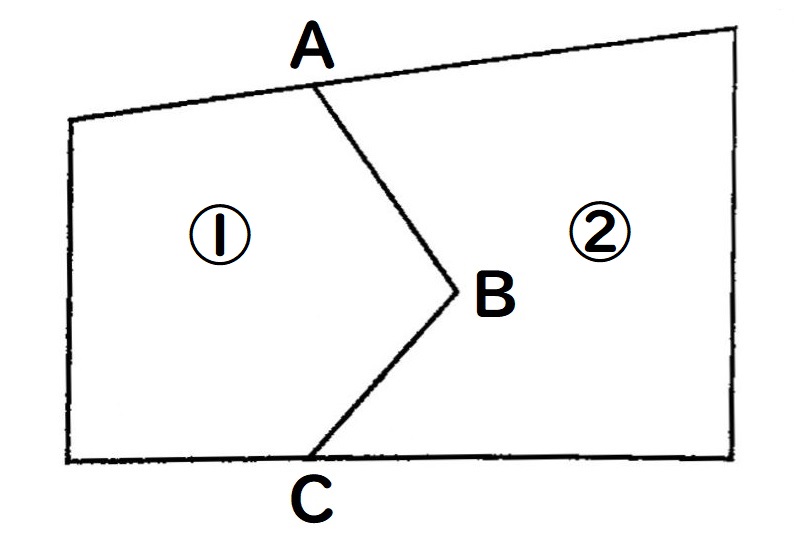
例題
それぞれの土地の
解き方のポイントは
② 図を描く。
③ 図に条件を書き込む。
ポイント①:問題文を小分けにして読む
問題文を小分けにして読むことで
条件はなにか?
何を答えるのか?
がはっきりします。
小分けにするときは、
アンダーラインなどで
印を付けていくと
分かりやすくなります。

●境界線ABCで、①と②に2分割
●点Aを通る直線で境界線引き直し
●面積変えない
になります。
ポイント②:図を描く


書き込むとさらに見にくくなるんです。
ポイント③:図に条件を書きこむ
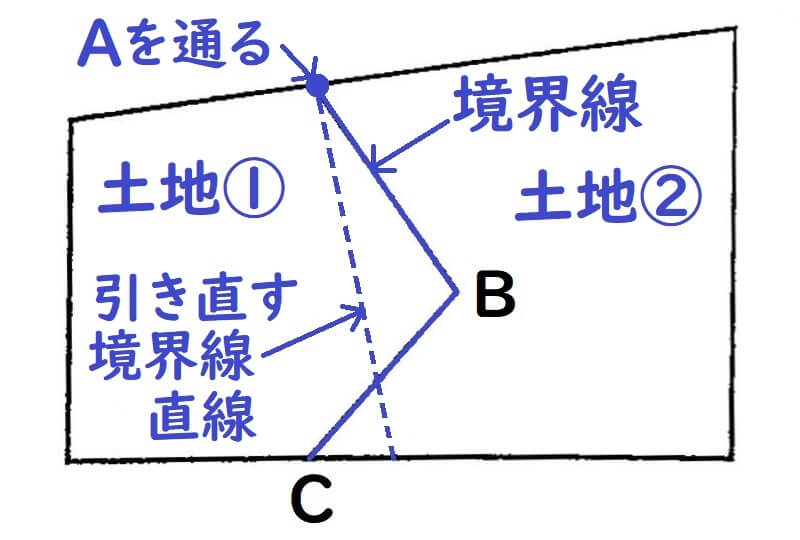
面積は変えない!
仕上げ:勉強したことをもとに解いていく
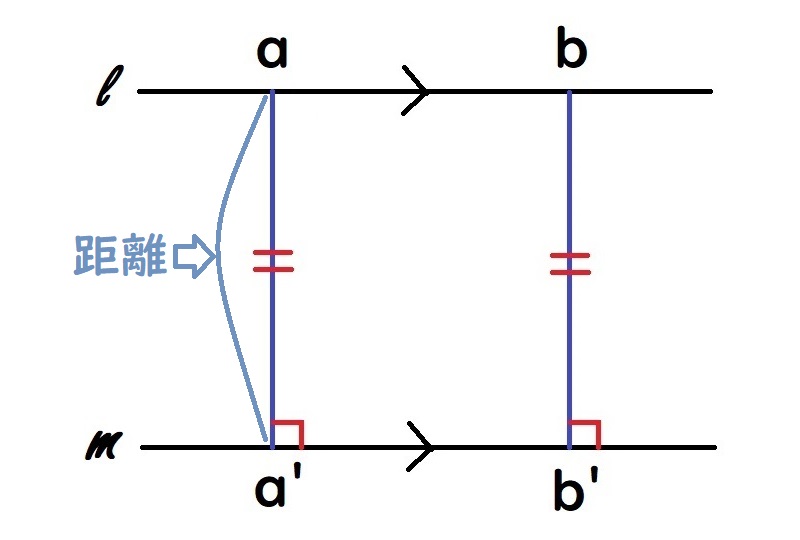
平行(矢印のような記号)な
●二つの直線の間に引かれた
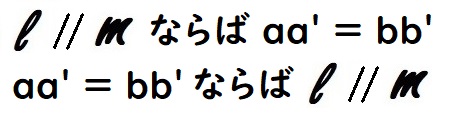
もう一つは
“底辺が同じ長さの三角形の性質”。
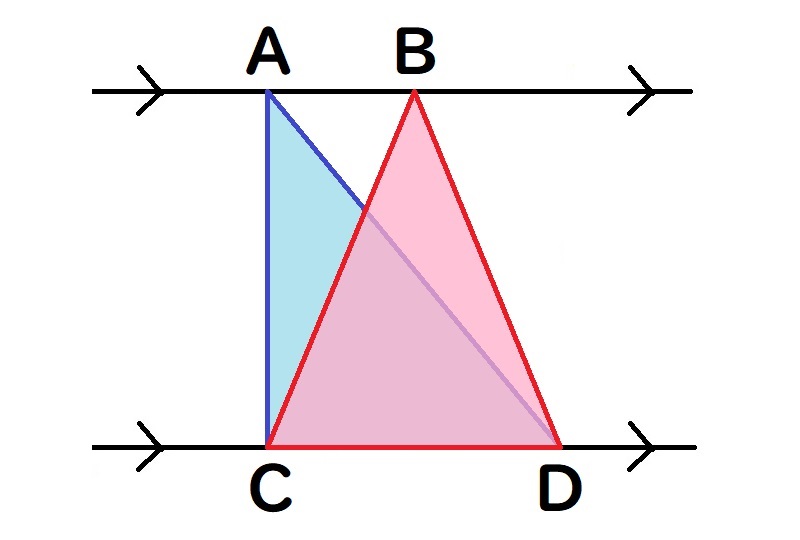 ●上の直線上の線分ABと、
●上の直線上の線分ABと、水色の三角形ACDと
上の直線上の線分ABと
△ACD=△BCD ならば AB // CD
この2つの性質をつかって、
もう一度、自分で描いた
図をいろんな方向から見直し
てみましょう。
すると
平行線と三角形をつかった解き方が
見えてくると思うのです。
解き方の手順
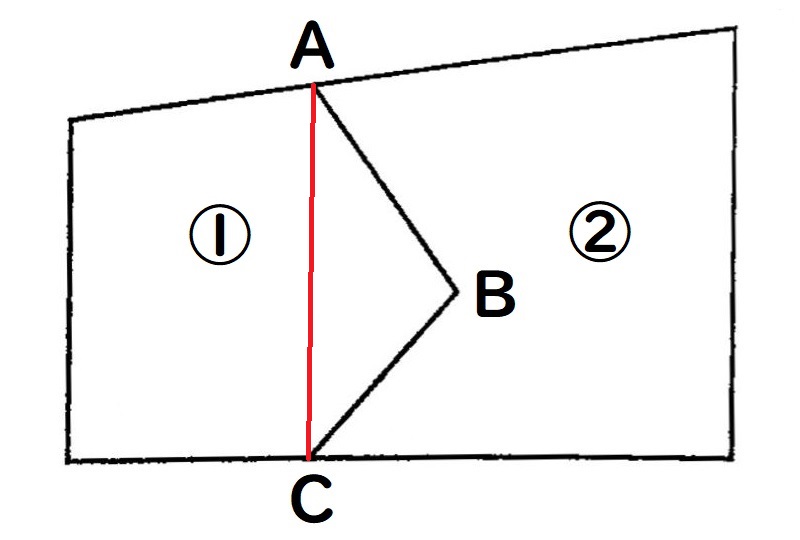
②Bを通って、直線ACと平行になる直線を引きます。
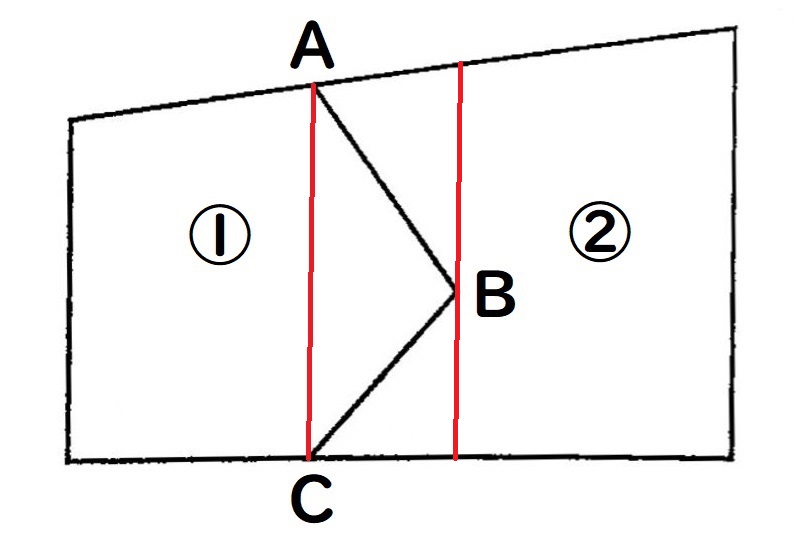
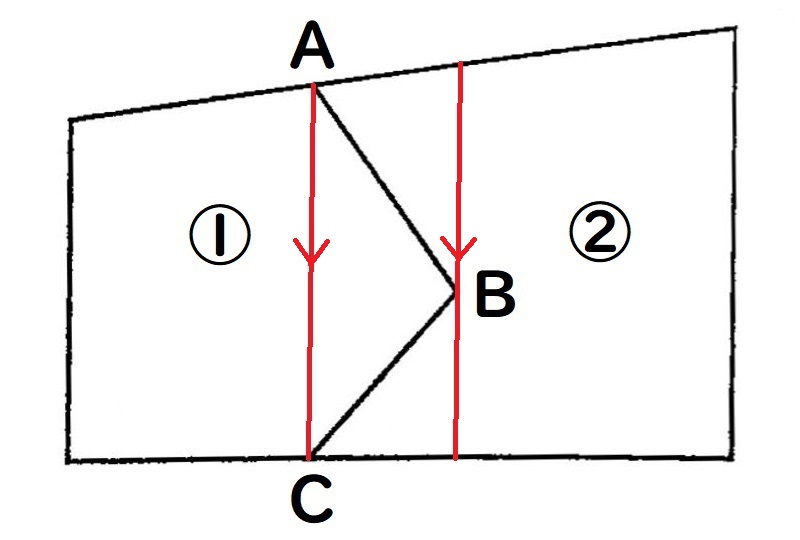
③直線ACを底辺とした三角形ABC(赤い線)ができます。
Bを通る直線と、四角形の底辺との交点をDとします。
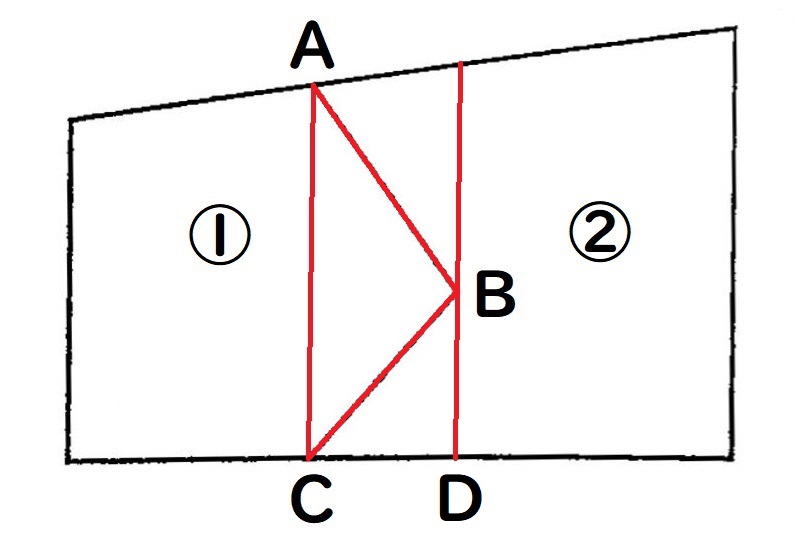
④Aを通る直線をDまで引くと、直線ACを底辺とした三角形ADC(水色の線)が描けます。
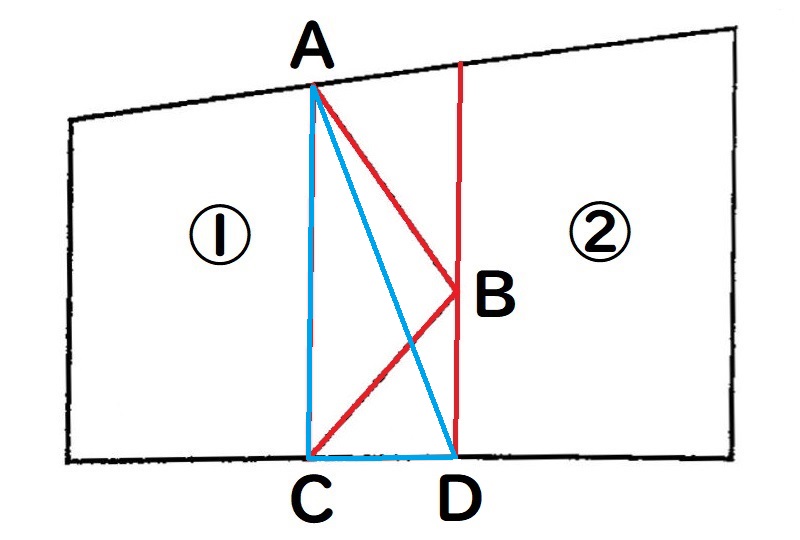
①の土地の一部である三角形ABCと
三角形ADCは、底辺と高さが同じなので面積も同じ。
境界線を
土地①と土地②の

条件を書いた図と変わらない♪


中学数学の図形。解き方のポイント|まとめ

こちらの記事では、
中学数学
図形問題の解き方ポイントと
「三角形と四角形」問題の
解き方を
例題を使って
説明してきました。
例題で取りあげたのは
“平行線と面積”のなかの
“等積変形”の問題。
記事の内容は、
・問題文を小分けにする
・図を描く
・図に条件を書き込む
の3つ。
●面積はそのままで形を変える
“等積変形”問題、
解き方のポイントにそって詳しく解説。
でした。

等積変形 問題演習
四角形ABCDと面積が等しい
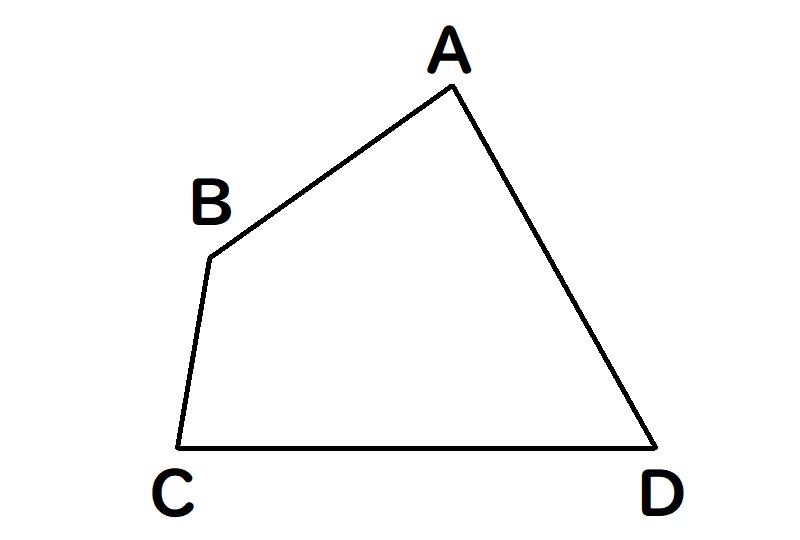


ここで取り上げた解き方を参考に、
数学図形問題の
実力アップにつなげて頂ければ
幸いです。
長文を最後までお読み頂き、
ありがとうございました。
図形の立体
苦手な生徒さん向けのポイントを
解説している記事は
こちらをご参照ください。
数学の文章問題の解き方、
ポイントを解説している記事も
併せてご参照ください。















