多くのサイトで紹介されている、高校の「偏差値」。 いろいろ調べている生徒さんほど、 サイトや資料によって希望高校の偏差値が少しずつ違っていることに気づくのではないでしょうか。
●偏差値を使うとわかるのは、テスト受験者の中での自分の位置
●偏差値を使うときの注意点
●まとめ：大切なのは「偏差値」の使い方
●豆知識：たとえ話（正規分布）
●開校５年半で、新潟県内トップ私立高校合格者を輩出。
●年評定平均：中学時代3.7→高校進学後4.9、4.8の塾生を輩出。
●サポートした不登校の卒塾生、大学へ進学。
●当ブログ、にほんブログ村カテゴリー「中学受験（個人塾）」
で、2020年6月から13ヶ月連続ランキング１位。
2020年3月開設15ヵ月目で月間４万PV超達成。
●元公立高校教員
●現役カウンセラー
AD
目次【タップでジャンプ】
偏差値とは？
「偏差値」は「ものさし」
まず実例で、偏差値とはどういうものなのか、見ていきます。 のんさんは、
偏差値は何を表すかというと、
●「平均点よりもどれだけ上か、下か、の度合いを表す」“ものさし”
なんです。
ですから、偏差値の真ん中は「50」。
平均点をとった人の偏差値は「50」なんです。
偏差値で成績のものさしにするときは「平均点との差」が重要になるわけです。
その試験を受けた人たちがとった点数の「ばらつき」＝「分散」＝「標準偏差」、も大事な要素になってきます。
ほとんどの人が、平均点の－３点から平均点＋３点におさまっているなら「ばらつきは小さい」（＝標準偏差が小さい）、
平均点の－40点から平均点＋40点なら「ばらつきは大きい」（＝標準偏差が大きい）となるわけです。
「標準偏差」については、こちらの方の記事もご参照されると良いと思います。
偏差値を使うと、何ができるのか？
偏差値を使ってできることは、●得点のばらつきがちがうテストの成績を比べられる
だから、同じ試験の受験者の中であれば、
科目が変わっても、
平均点が変わっても、
受験者数が違っていても、
「あなたはこのくらいの位置にいますよ。」と教えてくれるのです。
一般的なテストなら、偏差値は
25～75（20～80という人もいます）の範囲
にほぼ収まります。
もちろん、「あるグループの中での位置」なわけですから、
都道府県の模試（というグループ）、
学校の模試（というグループ）、
塾の模試（というグループ）…
受けた模試ごとに偏差値は変わってきます。
教科、受験者数、テストの難易度、受験者のレベルによっても、変わってくるわけです。
偏差値を使う時の注意点
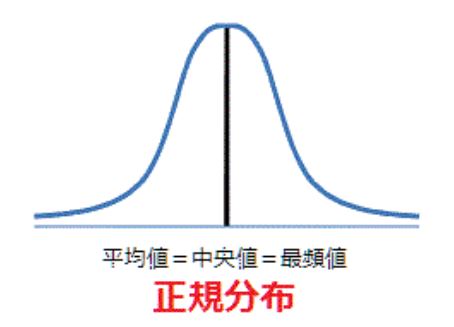
偏差値をグラフで表すと、「山」のような形になります。
グラフの形が富士山のようにきれいな形になれば利用価値は高いと言えます。
図のようなきれいな山型を「正規分布」なんて言ったりします。
出典：to-kei.net 統計学の学習用サイト"全人類がわかる統計学" 「正規分布の分かりやすいまとめ」
先ほどお話ししたように、
ばらつきが小さければ、山頂が急に高くなる山の形に、
ばらつきが大きければ、山頂が低く裾野の広い山の形
になるわけです。
この山がきれいな１つの山ならいいんですが、２つの山になるグラフもあったりします。
そんなグラフになる場合の偏差値は、利用価値がひくくなってしまいます。
上の図のような標準偏差の正規分布（きれいな山）を前提として、
100人の生徒さんの「偏差値からみた順位」をざっくりイメージ化してくださった土方（ひじかた、土に点）雅之氏。「わかりやすい！」と評判です！
ネットニュース等でも取り上げられていましたので、参考にされてみてはいかがでしょうか。
※逆の「順位から偏差値」は、判断できません。一方通行です。
画像は、下のリンクからご確認ください。
ツイート：『偏差値』は「順位でいうと、このあたり」と示すためのイメージ図誤解を恐れずざっくりまとめると、
●偏差値だけで高校や自分の成績の良し悪しは判断できない
●山が２つになるようなグラフになる「偏差値」は、あまり参考にならない
●偏差値の＋１～２、－１～２はよくあること。神経質にならない
一言でいうと
偏差値だけで、学校の価値も貴方の価値も、決まることはない
ので安心してください！ということなのです。
AD
偏差値とおさえておくべきポイント まとめ
こちらの記事では「偏差値とは？」、「偏差値を使うときのポイントは？」について見てきました。 - 内容は、
●偏差値は「成績をはかるものさし」の一種
●偏差値を使うとわかるのは、テスト受験者の中での自分の位置
●偏差値を使うときの注意点
偏差値のアップダウンをいちいち気にするより大切なことは、
どんな学校か、自分にぴったりの環境か、将来性は？など
●希望する高校を徹底的にリサーチする
●目標を決めたら、合格を勝ち取れるよう日々努力を続ける
これにつきると思うのです。
公立高校入試には、高校周辺の学区の生徒だけが挑戦するわけではありません。
ライバルの中の自分の位置と自分の頑張りを確認するために「偏差値」が知りたいときは、
必ず「都道府県単位の模試」を受けるようにしてください。
お役に立てましたら幸いです。
最後に「豆知識」として正規分布の「たとえ話」を追記しております。
ご参照頂ければ幸いです。
豆知識「たとえ話」（正規分布とは？）
記事本文の「偏差値」のばらつきをグラフ化したときに出てきた「正規分布」。
実際にはありえない話ですが、例として説明します。
たとえ話（正規分布）
のびのび中学校の２年生は、ちょうど100人！
●平均値（アベレージ）
数学の前期期末テストの100人の結果を全部足して、人数（100人）で割ると、
学年の平均点が出せます（「平均値」、算術平均）。
平均点は、50点。
●中央値（メジアン）
学年全員を得点順に並べたら、50位の人は51点、51位の人は49点だった。
学年人数が101人だったら、51位の人の点数が全員の真ん中の点数「中央値」になるけれど、
100人で偶数だから真ん中の人はいない。
そこで、50位の51点と51位の49点を足して２で割る。
結果、100人の「中央値」は、50点。
●最頻値（モード）
46点から54点までの人が一番多くて、100人中16人いた。
下限46点＋上限54点＝100点
100を２で割った50点が「最頻値」。
「最頻値」は、50点。
※ざっくり計算バージョンです。
正規分布は、このたとえ話のように、
平均値、中央値、最頻値の三つが同じになる（重なる）のです。
正規分布の特徴は、
●x軸が「しだいに近づいていく線（漸近線）」。
●ばらつき＝分散（標準偏差）が大きくなると、曲線の山は低くなり、左右に広がって平らに。
●ばらつき＝分散（標準偏差）が小さくなると、山は高くなり、よりとんがった形に。
になります。
公立高校一般入試のかなめ“内申点”につきましては、下記の記事をご参照ください。
教室の取り組みにつきましては、下記の記事をご参照ください。
